„Laboratórium 2 - 11. Mérés ellenőrző kérdései” változatai közötti eltérés
| (13 közbenső módosítás, amit 7 másik szerkesztő végzett, nincs mutatva) | |||
| 14. sor: | 14. sor: | ||
A PLC-k programfeldolgozása ciklikus működésű. A ciklus mindig egy startup | A PLC-k programfeldolgozása ciklikus működésű. A ciklus mindig egy startup | ||
blokkal (OB100 vagy | blokkal (OB100 vagy OB101) indul, ami RUN állapotba való átkapcsoláskor vagy | ||
újraindításkor hívódik meg. A blokk törli a belső változókat, a megfelelő memóriákat és | újraindításkor hívódik meg. A blokk törli a belső változókat, a megfelelő memóriákat és | ||
megszakítás kéréseket. | megszakítás kéréseket. | ||
| 31. sor: | 31. sor: | ||
Ellátott funkciók: | Ellátott funkciók: | ||
*Analóg kimenet: | *Analóg kimenet: | ||
** | **Fűtés vezérlése (PLC1) | ||
**Ventilátor vezérlése (PLC2) | **Ventilátor vezérlése (PLC2) (az új mérési elrendezésben csak 1 plc van, a ventilátor vezérlését egy PWM üzemmódú digitális kimenet végzi) | ||
*Analóg bemenet: | *Analóg bemenet: | ||
**Tranzisztor hőmérséklet (PLC1) | **Tranzisztor hőmérséklet (PLC1) | ||
| 40. sor: | 40. sor: | ||
A hűtőtönk hőmérsékletét illetve a teljesítmény tranzisztor tok-hőmérsékletét egy-egy | A hűtőtönk hőmérsékletét illetve a teljesítmény tranzisztor tok-hőmérsékletét egy-egy | ||
hőmérséklet-érzékelővel mérjük. A hűtőtönk hőmérsékletét | hőmérséklet-érzékelővel mérjük. A hűtőtönk hőmérsékletét a teljesítmény-tranzisztor áramának növelésével | ||
lehet növelni. A termikus folyamat gyorsítása érdekében kényszerhűtést alkalmazunk. | lehet növelni. A termikus folyamat gyorsítása érdekében kényszerhűtést alkalmazunk. | ||
| 53. sor: | 53. sor: | ||
Funkciók: | Funkciók: | ||
*Szabályozásra vonatkozó beállítások, szabályozó típusának kiválasztása, szabályozási paraméterek | *Szabályozásra vonatkozó beállítások, szabályozó típusának kiválasztása, szabályozási paraméterek | ||
*A kézi beavatkozójel, az alapjel és a | *A kézi beavatkozójel, az alapjel és a hűtőventilátor jelének beállítása | ||
*Hiba nyugtázása | *Hiba nyugtázása | ||
*Human Machine Interface | *Human Machine Interface | ||
| 167. sor: | 167. sor: | ||
==15. Adja meg egy folytonos PID szabályzó átvitel függvényét soros és párhuzamos realizációban!== | ==15. Adja meg egy folytonos PID szabályzó átvitel függvényét soros és párhuzamos realizációban!== | ||
Ideális PID szabályzó átviteli függvénye (párhuzamos realizációban): | |||
<math>W_{PID}(s)=A_P \cdot \left( 1 + {1 \over sT_i} + sT_D \right) = {A_P \over T_i} \cdot {1 + sT_i + s^2 T_i T_D \over s }</math> | |||
Mivel ez a gyakorlatban nem realizálható, ezért közelítő PID szabályzót alkalmazunk: | |||
<math>W_{PID}(s)=A_P \cdot \left( 1 + {1 \over sT_i} + {sT_D \over 1 +sT_C} \right) = | |||
{A_P \over T_i} \cdot {1 + s(T_i + T_C) + s^2 T_i( T_D +T_C) \over s \cdot (1+sT_C) }</math> | |||
==16. Hogyan befolyásolja a beavatkozójel korlátozása a szabályozási kör működését?== | ==16. Hogyan befolyásolja a beavatkozójel korlátozása a szabályozási kör működését?== | ||
Ha korlátozzuk a beavatkozó jelet, akkor később áll be a szabályozási kör. Tehát nő a beállási | |||
tranziens, a beállás lengő jellegű lesz. A túllövés mértéke is növekedhet. | |||
==17. Hogyan valósítható meg pont-pont összeköttetés feltételes bevitellel, lazán csatolt rendszerekben?== | ==17. Hogyan valósítható meg pont-pont összeköttetés feltételes bevitellel, lazán csatolt rendszerekben?== | ||
Van két független eszköz, amelynek vannak közös perifériái. | |||
Például a mérésünk keretei között azt akarjuk, hogy az egyik eszköz tudjon a másikkal kommunikálni, mert szeretnénk, ha az a PLC, amelyet programozni tudunk (PLC1), tudja vezérelni a ventilátorhűtést (amit viszont a PLC0 végez). | |||
Egy közös perifériát használunk a kommunikációra. | |||
PLC1 fogja magát, beír valamit ebbe a perifériába (képzeld el úgy, mint egy I/O write). A PLC0 ezt észreveszi, hogy küldtek neki valamit, kiveszi az üzenetet és értelmezi. | PLC1 fogja magát, beír valamit ebbe a perifériába (képzeld el úgy, mint egy I/O write). A PLC0 ezt észreveszi, hogy küldtek neki valamit, kiveszi az üzenetet és értelmezi. | ||
A nyalánkságok: | A nyalánkságok: Hogyan veszi észre PLC0, hogy üzenetet kapott? Például úgy, hogy van egy másik periféria (set-reset jellegű), amit ha üzenetet küldesz, akkor 1-be billented, amikor elveszed az üzenetet, akkor 0-ba. | ||
[[File:Labor2_mérés11_ábra3.JPG|600px]] | |||
==18. Milyen memóriaszegmensei vannak a Siemens 314C-2DP kompakt PLC-nek?== | ==18. Milyen memóriaszegmensei vannak a Siemens 314C-2DP kompakt PLC-nek?== | ||
A PLC-ben rendelkezésre álló memória alapvetően három részre osztható: | |||
*A memóriakártyán (MMC) található részben tárolódik minden programkód, az adatblokkok és a konfigurációs adatok. | |||
*A RAM memória tartalmazza a mindenkori futó programot és annak adatait. | |||
*A rendszer memória további konfigurációs adatokat, valamint a be- és kimenetek aktuális értékeit tárolja. | |||
==19. Adja meg az ARX modell kifejezését!== | ==19. Adja meg az ARX modell kifejezését!== | ||
Legyen egy mintavételezett diszkrét idejő folyamat differenciaegyenlete a következő: | |||
<math>y[k]+a_1y[k-1]+...+a_{na}y[k-na]=b_1u[k-1-nd]+...+b_{nb}u[k-nb-nd]</math> | |||
Ahol <math>k=0,1,2,3...</math> a diszkrét időpontokat jelöli, <math>y[k]</math> a folyamat kimenőjele, <math>u[k]</math> a bemenőjele, <math>nd</math> a holtidő, továbbá <math>\left\{a_i,b_i \right\}</math> a folyamat modelljének paraméterei. | |||
A fenti összefüggés átírható az úgynevezett ARX alakra: | |||
<math>y[k]={B\left( z^{-1} \right) \over A\left( z^{-1} \right)} \cdot u[k-nd]</math> | |||
==20. Milyen költségfüggvényt használ a Matlab ''arx'' utasítás?== | ==20. Milyen költségfüggvényt használ a Matlab ''arx'' utasítás?== | ||
Az ''arx'' utasítás a legkisebb négyzetes (LS = Least Squares) költségfüggvényt használja. | |||
A legkisebb négyzetek módszerének alkalmazásakor a rendelkezésre álló <math>t=1...N</math> bemeneti-kimeneti mintapár ismeretében keressük az <math>\left\{ \hat{a}_i, \hat{b}_i\right\}</math> becsült paramétereket olyan formában, hogy a modell kimenete és a tényleges mért kimenet közötti <math>e(t)</math> eltérések négyzetének <math>J</math> összege (más szóval veszteségfüggvény) minimális legyen: | |||
<math>J=\sum_{t=na+nk+1}^N\limits \left[ e(t) \right]^2</math> | |||
[[ | [[Kategória:Villamosmérnök]] | ||
A lap jelenlegi, 2018. március 23., 19:12-kori változata
1. Mi a PLC és mire lehet használni?
A PLC egy olyan számítógép, amelyet architektúráját, működési rendszerét, programozási nyelvét és konstrukcióját tekintve gyártási folyamatok vezérlésére illetve szabályozására fejlesztettek ki. A PLC analóg és digitális jelekkel csatlakozik a folyamathoz, programozása speciális programozó készülékkel vagy hagyományos PC-vel történik.
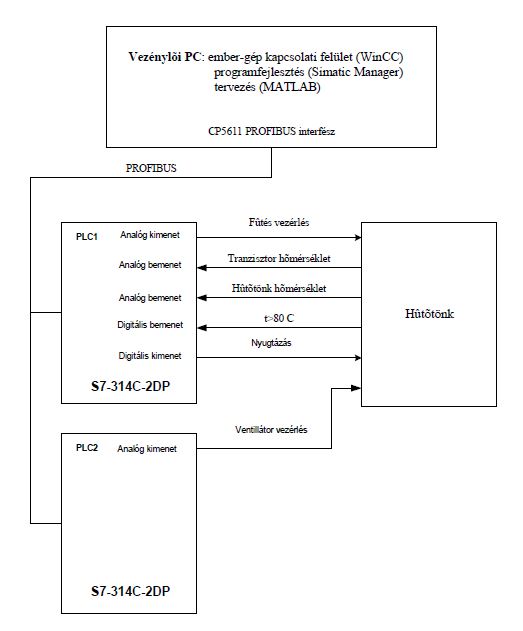
2. Rajzolja fel a mérési elrendezés blokkvázlatát!
3. Mit jelent az, hogy a PLC programfeldolgozása ciklikus működésű? Ismertesse a PLC ciklikus programvezérlésének a lépéseit!
A PLC-k programfeldolgozása ciklikus működésű. A ciklus mindig egy startup blokkal (OB100 vagy OB101) indul, ami RUN állapotba való átkapcsoláskor vagy újraindításkor hívódik meg. A blokk törli a belső változókat, a megfelelő memóriákat és megszakítás kéréseket.
Egy programciklus az alábbi részekből áll:
- A ciklusidő-figyelés újraindítása
- A kimeneti értékek táblájának (PIQ) kiírása a kimeneti kártyákra
- A bemeneti jelek állapotának lekérdezése és a bemeneti értékek táblájának (PII) aktualizálása
- A felhasználói program végrehajtása a benne lévő utasításokkal (azaz az OB1 blokk meghívása).
4. Milyen jelszintűek a PLC analóg ki- és bemenetei és ezek milyen funkciót látnak el a mérési elrendezésben?
Az illesztő kártya analóg ki- és bemenetei mindkét irányban 0-10 V-os jelszintűek. A bemenetek bemeneti ellenállása 100 kOhm. A kimenetek maximális terhelő árama 10 mA.
Ellátott funkciók:
- Analóg kimenet:
- Fűtés vezérlése (PLC1)
- Ventilátor vezérlése (PLC2) (az új mérési elrendezésben csak 1 plc van, a ventilátor vezérlését egy PWM üzemmódú digitális kimenet végzi)
- Analóg bemenet:
- Tranzisztor hőmérséklet (PLC1)
- Hűtőtönk hőmérséklet (PLC1)
5. Mivel mérjük a hűtőtönk hőmérsékletét? Hogyan tudjuk növelni illetve csökkenteni a hűtőtönk hőmérsékletét?
A hűtőtönk hőmérsékletét illetve a teljesítmény tranzisztor tok-hőmérsékletét egy-egy hőmérséklet-érzékelővel mérjük. A hűtőtönk hőmérsékletét a teljesítmény-tranzisztor áramának növelésével lehet növelni. A termikus folyamat gyorsítása érdekében kényszerhűtést alkalmazunk.
6. Milyen funkciókat valósít meg a mérési elrendezésben a WinCC operációs rendszer?
A WinCC operációs rendszer a folyamatirányítási feladatok ember-gép kapcsolati felületét (HMI = Human Machine Interface) hivatott megvalósítani. Grafikus felülete lehetőséget biztosít, hogy elemenként tetszőlegesen építsük fel az operátori felületet. Lehetőséget nyújt egy folyamat jeleinek megjelenítésére, vezérlésére. A WinCC változók segítségével kapcsolódik a PLC-k paramétereit és mérési adatait tartalmazó blokkhoz.
Funkciók:
- Szabályozásra vonatkozó beállítások, szabályozó típusának kiválasztása, szabályozási paraméterek
- A kézi beavatkozójel, az alapjel és a hűtőventilátor jelének beállítása
- Hiba nyugtázása
- Human Machine Interface
7. Milyen funkciókat valósít meg a mérési elrendezésben a Simatic Manager?
A Siemens S7-300-as típusú PLC-khez szükséges programokat a Simatic Manager szoftver segítségével tudjuk megírni, szimulálni, a PLC-t felprogramozni. A szoftver kezelőfelülete a Simatic Manager, mely használatával képesek vagyunk beállítások, konfigurációk, fejlesztések, szimulációk és sok más dolog elvégzésére. A STEP7 szoftver több, alacsonyabb és magasabb szintű programozási nyelvet ismer.
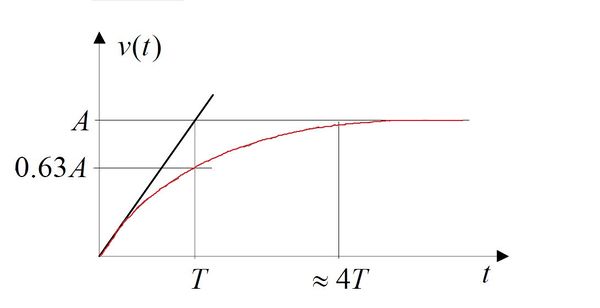
8. Adja meg az egytárolós arányos tag átviteli függvényét és ábrázolja az ugrásválaszát!
Az egytárolós tag átviteli függvénye - Vigyázat: Az sem szabad elfelejteni, hogy van egy A erősítése is!
Az egytárolós tag ugrásválasza:
Az egytárolós tag ugrásválaszának ábrázolása:
9. Adja meg a folytonos PI szabályzó átviteli függvényét! Hány paramétere van a szabályzónak és ezeket hogyan választjuk meg?
A PI típusú szabályzó átviteli függvénye:
A szabályozó erősítése és integrálási időállandója pozitív számok.
A szabályzó a körerősítést -szeresére változtatja, a szabályozási kör típusszámát pedig eggyel növeli.
A szabályzó egy zérust is bevisz a felnyitott kör átviteli függvényébe.
Paraméterek:
- Így tudunk előírt fázistartalékra tervezni.
- Ezzel kiejthetjük a szakasz leglassabb pólusát, biztosítva így a gyorsabb működést.
10. Mit nevezünk a rendszer típusszámának? Milyen hibával követi az egységugrás alapjelet egy 0 illetve egy 1 típusú rendszer?
A szakasz átviteli függvénye:
A felnyitott kör függvény átviteli függvénye soros kompenzátor és egységnyi merev negatív visszacsatolás esetén:
Ahol , a körerősítés és a szabályozási kör típusszáma. Tehát a típusszám a szabályozási körben található integrátorok száma.
Statikus/maradó hiba:
- esetén
- esetén
11. Milyen tervezési (minőségi) előírásokat ismer egy zárt szabályozási kör jellemzésére?
- Statikus hiba
- Túllövés
- Beállási idő (5%-os tartományba kerülésig eltelt idő)
- Felfutási idő
- Fázistartalék
- Vágási (metszési) körfrekvencia
- A beavatkozójel maximális értéke adott alapjel esetén
12. Mikor stabilis egy folytonos illetve egy mintavételes lineáris rendszer?
- Folytonos lineáris rendszer stabilis: A zárt kör minden sajátértéke a bal oldali félsíkon van: Re{s}<0
- Mintavételes lineáris rendszer stabilis: A zárt kör minden sajátértéke a komplex számsíkon az egységkörön belül van: |z|<1
13. Adja meg az integrátor tulajdonságait!
Átviteli függvénye:
Átmeneti függvénye:
Amplitúdó spektruma:
Fázisfüggvénye:
Jellemzői:
- Dinamikus tag - Kimenő jele a bemenő jelének idő szerinti integrálja.
- Kimenő jele időben lineárisan változik, ha a bemenő jele állandó.
- Kimenő jele csak akkor állandó, ha a bemenő jele 0.
- A kimenő jel véges bemenő jel eseten nem ugorhat.
- Memória tulajdonsága van.
14. Adja meg egy diszkrét PID szabályzó impulzusátviteli függvényét és differencia egyenletét!
A diszkrét PID szabályzó impulzusátviteli függvénye - T a mintavételi periódusidő, s operátor közelítése BWD-vel, 1/s operátor közelítése RSR-rel:
Differencia egyenlete - u[k] a beavatkozó jel, e[k] pedig a hibajel:
A három paraméter pedig, könnyen meghatározható, ha a JR2-ből tanult módszerrel az átviteli karakterisztikából felírjuk a rendszeregyenletet:
15. Adja meg egy folytonos PID szabályzó átvitel függvényét soros és párhuzamos realizációban!
Ideális PID szabályzó átviteli függvénye (párhuzamos realizációban):
Mivel ez a gyakorlatban nem realizálható, ezért közelítő PID szabályzót alkalmazunk:
16. Hogyan befolyásolja a beavatkozójel korlátozása a szabályozási kör működését?
Ha korlátozzuk a beavatkozó jelet, akkor később áll be a szabályozási kör. Tehát nő a beállási tranziens, a beállás lengő jellegű lesz. A túllövés mértéke is növekedhet.
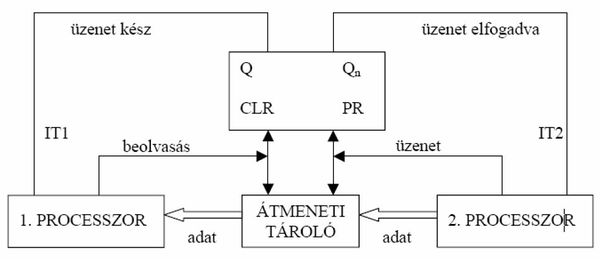
17. Hogyan valósítható meg pont-pont összeköttetés feltételes bevitellel, lazán csatolt rendszerekben?
Van két független eszköz, amelynek vannak közös perifériái.
Például a mérésünk keretei között azt akarjuk, hogy az egyik eszköz tudjon a másikkal kommunikálni, mert szeretnénk, ha az a PLC, amelyet programozni tudunk (PLC1), tudja vezérelni a ventilátorhűtést (amit viszont a PLC0 végez).
Egy közös perifériát használunk a kommunikációra.
PLC1 fogja magát, beír valamit ebbe a perifériába (képzeld el úgy, mint egy I/O write). A PLC0 ezt észreveszi, hogy küldtek neki valamit, kiveszi az üzenetet és értelmezi.
A nyalánkságok: Hogyan veszi észre PLC0, hogy üzenetet kapott? Például úgy, hogy van egy másik periféria (set-reset jellegű), amit ha üzenetet küldesz, akkor 1-be billented, amikor elveszed az üzenetet, akkor 0-ba.
18. Milyen memóriaszegmensei vannak a Siemens 314C-2DP kompakt PLC-nek?
A PLC-ben rendelkezésre álló memória alapvetően három részre osztható:
- A memóriakártyán (MMC) található részben tárolódik minden programkód, az adatblokkok és a konfigurációs adatok.
- A RAM memória tartalmazza a mindenkori futó programot és annak adatait.
- A rendszer memória további konfigurációs adatokat, valamint a be- és kimenetek aktuális értékeit tárolja.
19. Adja meg az ARX modell kifejezését!
Legyen egy mintavételezett diszkrét idejő folyamat differenciaegyenlete a következő:
Ahol a diszkrét időpontokat jelöli, a folyamat kimenőjele, a bemenőjele, a holtidő, továbbá a folyamat modelljének paraméterei.
A fenti összefüggés átírható az úgynevezett ARX alakra:
20. Milyen költségfüggvényt használ a Matlab arx utasítás?
Az arx utasítás a legkisebb négyzetes (LS = Least Squares) költségfüggvényt használja.
A legkisebb négyzetek módszerének alkalmazásakor a rendelkezésre álló bemeneti-kimeneti mintapár ismeretében keressük az becsült paramétereket olyan formában, hogy a modell kimenete és a tényleges mért kimenet közötti eltérések négyzetének összege (más szóval veszteségfüggvény) minimális legyen: