„Bode-diagram kézi rajzolása” változatai közötti eltérés
| (18 közbenső módosítás, amit 6 másik szerkesztő végzett, nincs mutatva) | |||
| 11. sor: | 11. sor: | ||
<math> | <math> | ||
L(s) = {K \over s^i} \cdot {\ | L(s) = {K \over s^i} \cdot {\prod_{k} \left( {1 + sT_k} \right) \cdot \prod_{m} \left( 1 + s \cdot 2 \xi_m T_m + s^2 T_m^2 \right) \over | ||
\ | \prod_{l} \left( {1 + sT_l} \right) \cdot \prod_{n} \left( 1 + s \cdot 2 \xi_n T_n + s^2 T_n^2 \right)} | ||
</math> | </math> | ||
| 24. sor: | 24. sor: | ||
Először a számlálót és a nevezőt is szorzattá kell alakítani, aztán annyit emelünk ki, hogy az "s" nélküli tagok értéke 1 legyen: | Először a számlálót és a nevezőt is szorzattá kell alakítani, aztán annyit emelünk ki, hogy az "s" nélküli tagok értéke 1 legyen: | ||
<math>L(s)=\frac{10 \cdot (s+10)}{s^3+51s^ | <math>L(s)=\frac{10 \cdot (s+10)}{s^3+51s^2+50s}=10\frac{s+10}{s(s+1)(s+50)}=10\frac{10}{50}\frac{1+0.1s}{s(1+s)(1+0.02s)}={2 \over s} \cdot \frac{(1+0.1s)}{(1+s)(1+0.02s)}</math>. | ||
| 37. sor: | 37. sor: | ||
Pólusok - Azok a helyek, ahol a nevező értéke lesz 0: <math>p_1=0, \;p_2=-1, \;p_3=-50</math> | Pólusok - Azok a helyek, ahol a nevező értéke lesz 0: <math>p_1=0, \;p_2=-1, \;p_3=-50</math> | ||
=== 3. Fel/letörések meghatározása | === 3. Fel/letörések meghatározása === | ||
Ezek után készítsük el az alábbi táblázatot, melynek első sorában a pólusok és a zérusok abszolút értékük szerinti növekvő sorrendbe vannak rendezve (ezek lesznek a töréspontok): | Ezek után készítsük el az alábbi táblázatot, melynek első sorában a pólusok és a zérusok abszolút értékük szerinti növekvő sorrendbe vannak rendezve (ezek lesznek a töréspontok): | ||
| 77. sor: | 77. sor: | ||
=== 4. A görbe kezdő meredeksége === | === 4. A görbe kezdő meredeksége === | ||
Ha | Ha a rendszer tartalmaz integrátort (i>0), akkor a fenti képlet a kezdő meredekséget is tökéletesen megadja. Azaz 1 integrátornál a kezdő meredekség -20 dB/dek, 2 integrátornál -40 dB/dek... | ||
Ha azonban nincs | Ha azonban nincs integrátor a rendszerben (i=0), akkor az amplitúdó görbe kezdő meredeksége zérus, azaz egy vízszintes szakasszal indul. | ||
A fenti példában egyszeres integrátor van, azaz -20dB/dekád a kezdő meredekség. | A fenti példában egyszeres integrátor van, azaz -20dB/dekád a kezdő meredekség. | ||
| 85. sor: | 85. sor: | ||
(Ha esetleg olyan állna elő, hogy i<0, azaz a nincs 0 értékű pólus, de van legalább egy 0 értékű zérus, akkor a kezdő meredekség szintén a képlet szerint alakul. Azaz +20 dB/dek, +40 dB/dek.... ) | (Ha esetleg olyan állna elő, hogy i<0, azaz a nincs 0 értékű pólus, de van legalább egy 0 értékű zérus, akkor a kezdő meredekség szintén a képlet szerint alakul. Azaz +20 dB/dek, +40 dB/dek.... ) | ||
=== 5. Az omega tengely metszésének pontja | === 5. Az omega tengely metszésének pontja === | ||
Most már tudjuk, hogyan néz ki az aszimptotikus amplitúdó görbe menete, de még szükségünk van az <math>\omega</math> tengely metszéspontjára, azaz <math>\omega_c</math> vágási körfrekvencia értékére. | Most már tudjuk, hogyan néz ki az aszimptotikus amplitúdó görbe menete, de még szükségünk van az <math>\omega</math> tengely metszéspontjára, azaz <math>\omega_c</math> vágási körfrekvencia értékére. | ||
Ez legtöbb esetben a kezdeti meredekség és a körerősítés alapján meghatározható. Ha nincs integrátor a | Ez legtöbb esetben a kezdeti meredekség és a körerősítés alapján meghatározható. Ha nincs integrátor a rendszerben (i=0), akkor a kezdeti szakasz vízszintes, így ez a módszer sajnos nem használható. Ha azonban i>0, akkor tudjuk, hogy az integrátor egyenese (van annak meghosszabbítása) <math>\sqrt[i]{K}</math> körfrekvencián metszi az <math>\omega</math> tengelyt. Ha ez előtt a pont előtt nincs töréspont, akkor a tényleges amplitúdógörbe is itt fogja metszeni az <math>\omega</math> tengelyt. | ||
| 104. sor: | 104. sor: | ||
Felhasználható azonosság még, hogy az integrátor egyenese (vagy annak meghosszabbítása) <math>\omega=1</math> körfrekvencián <math>20 \cdot log(K)</math> értéket vesz fel dB-ben. | Felhasználható azonosság még, hogy az integrátor egyenese (vagy annak meghosszabbítása) <math>\omega=1</math> körfrekvencián <math>20 \cdot log(K)</math> értéket vesz fel dB-ben. | ||
=== 6. Amplitúdó-körfrekvencia görbe felrajzolása | === 6. Amplitúdó-körfrekvencia görbe felrajzolása === | ||
Itt az eddigieket kell összegyúrni eggyé. Először felrajzolod az görbe vonalát a megfelelő meredekségekkel (ezeket rá is kell írni) és törésekkel. Ezután behúzod az <math>\omega</math> tengelyt úgy, hogy már tudjuk a kiszámolt értékből, hogy az amplitúdó görbe melyik szakaszára (melyik két töréspont közé) esik a vágási körfrekvencia - Jelen esetben ez az 1 és az 10 közötti szakasz. Ezután jelölöd az <math>\omega</math> tengelyen a töréspontok értékeit és a vágási körfrekvencia értékét. Végül behúzod <math>|L(j\omega)|</math> tengelyt. | |||
[[File:Bode-diagram_amplitudo.jpg]] | |||
=== 7. Fázis-körfrekvencia görbe === | |||
Ezt a legegyszerűbb úgy megszerkeszteni, hogy az Y tengelyt felosztjuk 90°-onként. A fenti fel/letöréseknek megfelelően megy át a fázisgörbe egyik sávról a másikra. Ha feltörik, akkor az érték 90°-al nő, ha letörik, akkor 90°-al csökken. Értelemszerűen, ha többszörös multiplicitású pólus/zérus okozza a törést, akkor annyiszor 90°-al változik a fázisgörbe menete, ahányszoros multiplicitású a törést kiváltó pólus/zérus. | |||
Ez viszont nem egyik pillanatról a másikba megy végbe, hanem "átmenetszerűen", rajzban ez azt jelenti, hogy a törésponti körfrekvencián már PONTOSAN félúton van az új állapot felé. | |||
[[File:Bode-diagram fazis.jpg]] | |||
=== 8. Fázisgörbe kezdőértéke === | |||
Ez a rendszer típusszámán (i) és a körerősítésén (K) múlik: | |||
# Ha a K körerősítés pozitív, akkor a kezdőérték 0°, ha negatív, akkor -180° | |||
# A fent kikalkulált kezdőértéket az integrátorok (-i*90°)-al változtatják meg: | |||
#* Ha nincs integrátor (i=0), akkor pozitív K esetén 0°, negatív K esetén -180° | |||
#* Ha egy integrátor van (i=1), akkor pozitív K esetén -90°, negatív K esetén -270° | |||
#* Ha két integrátor van (i=2), akkor pozitív K esetén -180°, negatív K esetén -360° = 0° | |||
#* Ha a nevezőben nincs integrátor, de van 0 értékű zérus (i= -1), akkor pozitív K esetén +90°, negatív K esetén -90° | |||
=== 9. Fázistartalék(többlet) meghatározása === | |||
A fázistartalék <math>\varphi_t</math> értéke megadja, hogy a fázisgörbe a vágási körfrekvencián mennyivel van -180° felett. Azaz ahol az amplitúdó görbe metszi az <math>\omega</math> tengelyt, ott megnézed a <math>\varphi (\omega)</math> görbe értéke mennyivel van -180° felett. | |||
Ennek a közelítő leolvasásához célszerű egy jó aszimptotikus amplitúdó görbét rajzolni és alá egy fázisgörbét, bár erről csak az látszik általában hogy a fázistartalék pozitív, avagy negatív. Jelen esetben sajnos még ezt is nehézkes eldönteni... | |||
Szerencsére a fázisgörbe függvénye egzaktul megadható az átviteli függvényből, az alábbi általános képlet alapján - ha K negatív, akkor még 180°-ot le kell vonni belőle: | |||
<math>\varphi(\omega) = -i \cdot 90^{\circ} + \sum_{k} arctg \left( {1\over |z_k|} \cdot \omega \right) - \sum_{l} arctg \left( {1\over |p_l|} \cdot \omega \right)</math> | |||
{| | |||
| Típusszám || 0 || 1 || 2 | A mi esetünkben: | ||
<math>\varphi(\omega) = -1 \cdot 90^{\circ} + arctg \left( {1\over |-10|} \cdot \omega \right) - arctg \left( {1\over |-1|} \cdot \omega \right) - arctg \left( {1\over |-50|} \cdot \omega \right)=</math> | |||
<math> | |||
=-90^{\circ} +arctg \left( 0.1 \cdot \omega \right) - arctg \left( \omega \right) - arctg \left( 0.02 \cdot \omega \right) | |||
</math> | |||
Tehát a fázistartalék: | |||
<math> | |||
\varphi_t=\varphi(\omega_c)+180^{\circ}=180^{\circ}-90^{\circ} +arctg \left( 0.1 \cdot \omega_c \right) - arctg \left( \omega_c \right) - arctg \left( 0.02 \cdot \omega_c \right) \approx | |||
</math> | |||
<math> | |||
\approx 90^{\circ} +arctg \left( 0.1 \cdot \sqrt{2} \right) - arctg \left( \sqrt{2} \right) - arctg \left( 0.02 \cdot \sqrt{2} \right) = | |||
</math> | |||
<math> | |||
= 90^{\circ} +arctg \left( 0.1414 \right) - arctg \left( 1.414 \right) - arctg \left( 0.02828 \right) | |||
</math> | |||
Felhasználva az alábbi közelítéseket: | |||
<math>arctg(1)=45^{\circ}, arctg(0.1) \approx 5^{\circ}, arctg(10) \approx 85^{\circ}</math> | |||
<math>\varphi_t \approx 90^{\circ} + 5^{\circ} - 55^{\circ} - 0^{\circ} = 40^{\circ} </math> | |||
=== 10. Fázis-körfrekvencia görbe felrajzolása === | |||
Az itt lévő rajz kicsit csalóka, de a görbe menete jól látszik. A fázistartalék viszont +40°! | |||
[[File:Bode-diagram fazis teljes.jpg]] | |||
=== 11. A rendszer stabilitásvizsgálata === | |||
Stabilis-e a rendszer: Vagy azt nézed, hogy a fázistöbblet pozitív-e, vagy azt, hogy a jobboldali számsíkon van-e pólus - Ha nincs, akkor stabilis. | |||
=== 12. Statikus hiba === | |||
Megnézed az integrátorok számát, az adja a típusszámot, és azt a sort írod le a táblázatból ''(Lásd: könyv 140. oldal)''. | |||
{| class="wikitable" style="text-align:center" | |||
| '''Típusszám''' || 0 || 1 || 2 | |||
|- | |- | ||
| | | '''Egységugrás''' || <math>\frac{1}{1+K}</math> || 0 || 0 | ||
|- | |- | ||
| | | '''Sebességugrás''' || <math>\infty</math> || <math>\frac{1}{K}</math> || 0 | ||
|- | |- | ||
| | | '''Gyorsulásugrás''' || <math>\infty</math> || <math>\infty</math> || <math>\frac{1}{K}</math> | ||
|} | |} | ||
| 151. sor: | 200. sor: | ||
[[Kategória: | [[Kategória:Villamosmérnök]] | ||
[[Kategória: | [[Kategória:Mérnök informatikus]] | ||
A lap jelenlegi, 2017. december 29., 15:09-kori változata
A Bode-diagram kézi rajzolása több tantárgyból is előjöhet. Ehhez nyújt segítséget az alábbi leírás, melyet Ndroo készített a Keviczky-féle Szabályozástechnika-könyv alapján.
A Bode-diagram készítésének lépései
1. Átviteli függvény átalakítása
Az aszimptotikus Bode-diagramm rajzolásához először "Bode normál alakra" kell hoznunk az átviteli függvényt:
Ebből az alakból leolvasható a rendszer körerősítése és típusszáma (integrátorok száma).
Ha tehát a feladatban ehhez hasonló alak van: , akkor át kell alakítani ilyen alakká:
Először a számlálót és a nevezőt is szorzattá kell alakítani, aztán annyit emelünk ki, hogy az "s" nélküli tagok értéke 1 legyen:
.
Így minden tényező alakú lesz. Ha eleve így adták meg, akkor ezt a lépést ki kell hagyni.
Megjegyzés: Ha komplex konjugált gyökpárok is kijöttek volna a gyöktényezős felbontás során, akkor azok alakú tagokat hoztak volna be.
2. Pólusok/zérusok felírása
Zérusok - Azok a helyek ahol a számláló értéke 0 lesz:
Pólusok - Azok a helyek, ahol a nevező értéke lesz 0:
3. Fel/letörések meghatározása
Ezek után készítsük el az alábbi táblázatot, melynek első sorában a pólusok és a zérusok abszolút értékük szerinti növekvő sorrendbe vannak rendezve (ezek lesznek a töréspontok):
| Pólusok/zérusok abszolút értéke |
||||
|---|---|---|---|---|
| Index | +1 | +1 | -1 | +1 |
| Multiplicitás | 1 | 1 | 1 | 1 |
Az index értéke zérus esetén -1, pólus esetén +1.
A multiplicitás pedig azt jelenti, hogy „hányszoros gyök”. Azaz például ha a -1 háromszoros gyöke lenne a nevezőnek, akkor a multiplicitása 3 lenne. Továbbá a komplex konjugált pólus/zérus-párok esetén mindkét gyök abszolút értéke ugyanaz, így azok alapból 2-szeres multiplicitásúnak számítanak.
A jelleggörbe meredeksége a következő képlet szerint alakul:
Ez a meredekség érték mindig az előző meredekséghez hozzáadódik!
4. A görbe kezdő meredeksége
Ha a rendszer tartalmaz integrátort (i>0), akkor a fenti képlet a kezdő meredekséget is tökéletesen megadja. Azaz 1 integrátornál a kezdő meredekség -20 dB/dek, 2 integrátornál -40 dB/dek...
Ha azonban nincs integrátor a rendszerben (i=0), akkor az amplitúdó görbe kezdő meredeksége zérus, azaz egy vízszintes szakasszal indul.
A fenti példában egyszeres integrátor van, azaz -20dB/dekád a kezdő meredekség.
(Ha esetleg olyan állna elő, hogy i<0, azaz a nincs 0 értékű pólus, de van legalább egy 0 értékű zérus, akkor a kezdő meredekség szintén a képlet szerint alakul. Azaz +20 dB/dek, +40 dB/dek.... )
5. Az omega tengely metszésének pontja
Most már tudjuk, hogyan néz ki az aszimptotikus amplitúdó görbe menete, de még szükségünk van az tengely metszéspontjára, azaz vágási körfrekvencia értékére.
Ez legtöbb esetben a kezdeti meredekség és a körerősítés alapján meghatározható. Ha nincs integrátor a rendszerben (i=0), akkor a kezdeti szakasz vízszintes, így ez a módszer sajnos nem használható. Ha azonban i>0, akkor tudjuk, hogy az integrátor egyenese (van annak meghosszabbítása) körfrekvencián metszi az tengelyt. Ha ez előtt a pont előtt nincs töréspont, akkor a tényleges amplitúdógörbe is itt fogja metszeni az tengelyt.
Jelen esetünkben azonban 1 integrátor van, tehát az integrátor egyenese (vagy annak meghosszabbítása) K=2-nél metszi a tengelyt. Mivel azonban -nél az integrátor egyenesének kezdeti -20 dB/dek meredekségéhez -20 dB/dek hozzáadódik a képletnek megfelelően, tehát még előtt -40 dB/dek lesz a meredeksége, így a tényleges amplitúdó görbe nem 2-nél, hanem egy annál kisebb értéknél metszi az tengelyt!
Az integrátor egyenese körfrekvencián értéket vesz fel, hiszen dekád távolság van az 1 és 2 körfrekvencia értékek között, és az integrátor egyenesének meredeksége. Tudjuk, hogy a tényleges amplitúdó görbe körfrekvenciától meredekséggel halad, tehát kiszámíthatjuk, hogy az amplitúdó görbe -nél metszi az tengelyt.
Előfordul még olyan eset is, amikor az amplitúdó görbe duplán törik az integrátor egyenesének tengelymetszete előtt, méghozzá úgy hogy például -20 dB/dek-ről vízszintes szakaszba megy át, majd újra -20 dB/dek-re törik le. Ilyenkor a vágási körfrekvencia annyi dekáddal nagyobb az integrátor egyenesének tengelymetszeti pontjánál, ahány dekád széles az amplitúdó görbe vízszintes szakasza.
Általánosan elmondható, hogy érdemes először lerajzolni a görbe menetét és logikázni az ismert pontok alapján. Geometriai úton legtöbb esetben kihozható egy ismert tengelymetszetből a vágási körfrekvencia, azonban figyelni kell hogy az Y tengely dB skálában van, míg az X tengely pedig dekád skálában.
Felhasználható azonosság még, hogy az integrátor egyenese (vagy annak meghosszabbítása) körfrekvencián értéket vesz fel dB-ben.
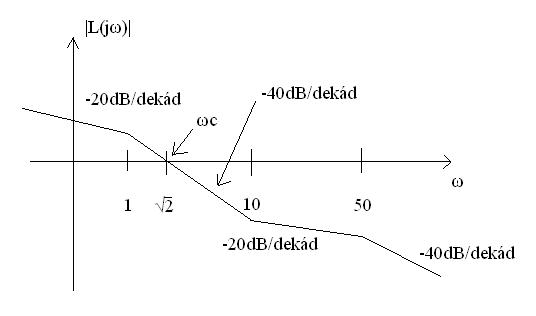
6. Amplitúdó-körfrekvencia görbe felrajzolása
Itt az eddigieket kell összegyúrni eggyé. Először felrajzolod az görbe vonalát a megfelelő meredekségekkel (ezeket rá is kell írni) és törésekkel. Ezután behúzod az tengelyt úgy, hogy már tudjuk a kiszámolt értékből, hogy az amplitúdó görbe melyik szakaszára (melyik két töréspont közé) esik a vágási körfrekvencia - Jelen esetben ez az 1 és az 10 közötti szakasz. Ezután jelölöd az tengelyen a töréspontok értékeit és a vágási körfrekvencia értékét. Végül behúzod tengelyt.
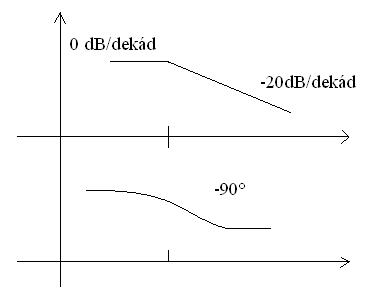
7. Fázis-körfrekvencia görbe
Ezt a legegyszerűbb úgy megszerkeszteni, hogy az Y tengelyt felosztjuk 90°-onként. A fenti fel/letöréseknek megfelelően megy át a fázisgörbe egyik sávról a másikra. Ha feltörik, akkor az érték 90°-al nő, ha letörik, akkor 90°-al csökken. Értelemszerűen, ha többszörös multiplicitású pólus/zérus okozza a törést, akkor annyiszor 90°-al változik a fázisgörbe menete, ahányszoros multiplicitású a törést kiváltó pólus/zérus.
Ez viszont nem egyik pillanatról a másikba megy végbe, hanem "átmenetszerűen", rajzban ez azt jelenti, hogy a törésponti körfrekvencián már PONTOSAN félúton van az új állapot felé.
8. Fázisgörbe kezdőértéke
Ez a rendszer típusszámán (i) és a körerősítésén (K) múlik:
- Ha a K körerősítés pozitív, akkor a kezdőérték 0°, ha negatív, akkor -180°
- A fent kikalkulált kezdőértéket az integrátorok (-i*90°)-al változtatják meg:
- Ha nincs integrátor (i=0), akkor pozitív K esetén 0°, negatív K esetén -180°
- Ha egy integrátor van (i=1), akkor pozitív K esetén -90°, negatív K esetén -270°
- Ha két integrátor van (i=2), akkor pozitív K esetén -180°, negatív K esetén -360° = 0°
- Ha a nevezőben nincs integrátor, de van 0 értékű zérus (i= -1), akkor pozitív K esetén +90°, negatív K esetén -90°
9. Fázistartalék(többlet) meghatározása
A fázistartalék értéke megadja, hogy a fázisgörbe a vágási körfrekvencián mennyivel van -180° felett. Azaz ahol az amplitúdó görbe metszi az tengelyt, ott megnézed a görbe értéke mennyivel van -180° felett.
Ennek a közelítő leolvasásához célszerű egy jó aszimptotikus amplitúdó görbét rajzolni és alá egy fázisgörbét, bár erről csak az látszik általában hogy a fázistartalék pozitív, avagy negatív. Jelen esetben sajnos még ezt is nehézkes eldönteni...
Szerencsére a fázisgörbe függvénye egzaktul megadható az átviteli függvényből, az alábbi általános képlet alapján - ha K negatív, akkor még 180°-ot le kell vonni belőle:
A mi esetünkben:
Tehát a fázistartalék:
Felhasználva az alábbi közelítéseket:
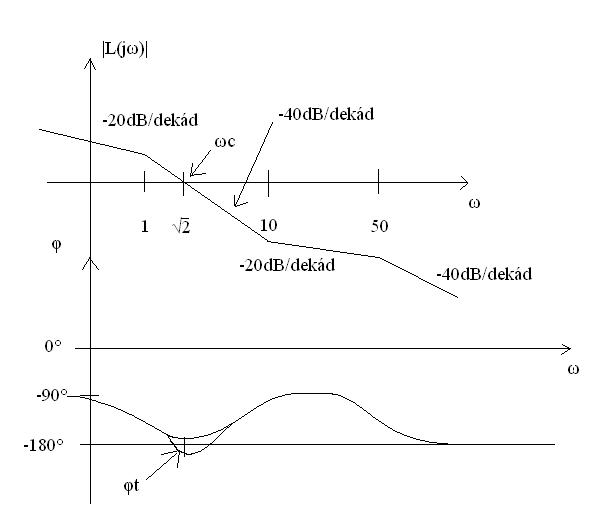
10. Fázis-körfrekvencia görbe felrajzolása
Az itt lévő rajz kicsit csalóka, de a görbe menete jól látszik. A fázistartalék viszont +40°!
11. A rendszer stabilitásvizsgálata
Stabilis-e a rendszer: Vagy azt nézed, hogy a fázistöbblet pozitív-e, vagy azt, hogy a jobboldali számsíkon van-e pólus - Ha nincs, akkor stabilis.
12. Statikus hiba
Megnézed az integrátorok számát, az adja a típusszámot, és azt a sort írod le a táblázatból (Lásd: könyv 140. oldal).
| Típusszám | 0 | 1 | 2 |
| Egységugrás | 0 | 0 | |
| Sebességugrás | 0 | ||
| Gyorsulásugrás |
- 0 jelentése: hiba nélkül követi
- jelentése: nem tudja követni