„Infokommunikáció - Vizsga, 2014.01.07.” változatai közötti eltérés
aNincs szerkesztési összefoglaló |
aNincs szerkesztési összefoglaló |
||
| (12 közbenső módosítás, amit 5 másik szerkesztő végzett, nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
*01: 01110 | *01: 01110 | ||
*10: 10101 | *10: 10101 | ||
*11: | *11: 11011 | ||
'''a) Adja meg a kód szisztematikus generátormátrixát! v=(01010) vett szó esetén melyik kódszó lett kiküldve a legnagyobb valószínűséggel?''' | '''a) Adja meg a kód szisztematikus generátormátrixát! v=(01010) vett szó esetén melyik kódszó lett kiküldve a legnagyobb valószínűséggel?''' | ||
| 41. sor: | 41. sor: | ||
{{Rejtett | {{Rejtett | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg= | |szöveg=a modulált jel alakja: <math>s(t)=U\cdot cos(2\pi{f_v}+m(t)),</math> ahol <math>m(t)={\Phi_D}\cdot sin(2\pi{f_m}t) </math> | ||
Az oszcilloszkóp képről leolvasható adatok: | |||
<math>{f_v}=50kHz</math> | |||
<math>{f_m}=2.5kHz</math> | |||
<math>U=\frac{14.8V}{2}=7.4V</math> | |||
<math>\Phi_D=\frac{4}{2}=2 rad</math> a moduláló jel amplitúdója | |||
<math>{f_D}=\frac{1}{2\pi}\cdot max(|m'(t)|)=\frac{1}{2\pi}\Phi_D\cdot 2\pi{f_m}=2\cdot 2.5kHz=5kHz</math> | |||
}} | }} | ||
| 47. sor: | 61. sor: | ||
{{Rejtett | {{Rejtett | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg=Pl: számláló típusú demodulátort. | |szöveg=Pl: számláló típusú demodulátort.<br\>[[Kép:Infokomm vizsga 20140107-2.png|500px]] | ||
}} | }} | ||
| 55. sor: | 69. sor: | ||
{{Rejtett | {{Rejtett | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg=<math>|E_r|=2 | |szöveg=<math>|E_r|=2 \cdot |E_0| \cdot \left|\sin \left( \pi \cdot \frac{2 \cdot h_t \cdot h_r}{\lambda \cdot r}\right)\right|</math> Az interferenciazóna határán a szinusz argumentuma pontosan <math>\frac{\pi}{2}</math>, tehát <math>|E_{rmax}|=2 \cdot |E_0|</math>. Ha felére csökkentjük h<sub>r</sub> értékét, a szinusz argumentuma is feleződik. <math>|E_r|=2 \cdot |E_0| \cdot \sin\left(\frac{\pi}{4}\right)=2 \cdot |E_0| \cdot \frac{\sqrt{2}}{2}=|E_{rmax}| \cdot \frac{\sqrt{2}}{2}</math> | ||
A teljesítmény a térerősség négyzetével arányos, tehát az eredeti állapothoz képest feleződni fog, ami '''3 dB-es csökkenést''' jelent. | A teljesítmény a térerősség négyzetével arányos, tehát az eredeti állapothoz képest feleződni fog, ami '''3 dB-es csökkenést''' jelent. | ||
| 95. sor: | 109. sor: | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg=Felső keverés: <math>F_o > F_v</math>, ahol F<sub>v</sub> az adó frekvenciája.<br\> | |szöveg=Felső keverés: <math>F_o > F_v</math>, ahol F<sub>v</sub> az adó frekvenciája.<br\> | ||
<math>F_o=F_v+f_{KF}=107+10.7= | <math>F_o=F_v+f_{KF}=107+10.7=117.7 MHz</math> | ||
}} | }} | ||
| 116. sor: | 130. sor: | ||
{{Rejtett | {{Rejtett | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg=A mintavételezés során | |szöveg=A mintavételezés során a bemenő szűrő által leszűrt jelünk spektruma f<sub>s</sub> egész számú többszörösei körül ugyanúgy megjelenik, ez hozza be a 7 és 9 kHz-es komponenseket a kimeneten (amiket a bemenő szűrő alapvetően levágott). A mintavételi frekvencia egész biztosan 2n MHz alakú, ahol n egész szám. Mivel a bemenő szűrő csak az alapharmonikust és a harmadik felharmonikust engedte át, a mintavételi frekvenciától plusz-mínusz 1 és 3 kHz-re jelennek meg komponensek. 2, 4, 6, 8 kHz-es mintavételezés esetén ez egészen biztosan behozna egy 5 kHz-es komponenst, olyan viszont nincs a kimeneten. A '''10 kHz-es mintavételi frekvencia''' viszont megfelel a követelményeknek: 10-1=9, 10-3=7, amennyiben a kimenő szűrő sávszélessége kisebb, mint 11 kHz (10+1=11, 10+3=13 kHz-es komponensek levágása miatt). | ||
}} | }} | ||
| 166. sor: | 180. sor: | ||
|szöveg=<math>\alpha=\frac{1}{3}</math><br\> | |szöveg=<math>\alpha=\frac{1}{3}</math><br\> | ||
Szimbólumsebesség: <math>8 MHz=2*\frac{1}{2T}*(1+\alpha) \Rightarrow \frac{1}{T}=8*10^6*\frac{3}{4}= 6 MBaud</math><br\> | Szimbólumsebesség: <math>8 MHz=2*\frac{1}{2T}*(1+\alpha) \Rightarrow \frac{1}{T}=8*10^6*\frac{3}{4}= 6 MBaud</math><br\> | ||
A 256QAM egy szimbólumban <math>\log_{2} | A 256QAM egy szimbólumban <math>\log_{2} 256=8</math> bitet visz át, a bitsebesség tehát <math>6 MBaud*8\frac{bit}{szimbolum}=48 Mbps</math><br\> | ||
A rendszerben <math>\frac{48}{1.5}=32</math> csatorna fér el. | A rendszerben <math>\frac{48}{1.5}=32</math> csatorna fér el. | ||
}} | }} | ||
| 173. sor: | 187. sor: | ||
{{Rejtett | {{Rejtett | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg= | |szöveg=*Előny: a 6 Mbps-es csatornán jobb képminőséget lehet szolgáltatni (akár már HD-t is) | ||
*Hátrány: több helyet foglal el egy csatorna -> kevesebb csatorna fér el egy raszterben | |||
}} | }} | ||
| 180. sor: | 195. sor: | ||
|mutatott='''Megoldás''' | |mutatott='''Megoldás''' | ||
|szöveg=*Előny: 6 helyett 10 bit átvitele egy jelzési időn belül, nagyobb bitsebesség. | |szöveg=*Előny: 6 helyett 10 bit átvitele egy jelzési időn belül, nagyobb bitsebesség. | ||
*Hátrány: nagyobb teljesítményigény | *Hátrány: nagyobb teljesítményigény, kisebb zajtűrés | ||
}} | }} | ||
| 189. sor: | 204. sor: | ||
|szöveg=Ha teljesül a Kraft-egyenlőtlenség: <math>\sum_{i=1}^N 2^{-l_i} \leq 1</math>, ahol l<sub>i</sub> az i-edik kódszó hossza, akkor lehet egyértelműen megfejthető kódot készíteni. | |szöveg=Ha teljesül a Kraft-egyenlőtlenség: <math>\sum_{i=1}^N 2^{-l_i} \leq 1</math>, ahol l<sub>i</sub> az i-edik kódszó hossza, akkor lehet egyértelműen megfejthető kódot készíteni. | ||
<math>2* | <math>2*{2^{-2}}+3*{2^{-3}}+4*{2^{-4}}=\frac{18}{16} > 1</math>, tehát '''nem lehetséges'''. | ||
}} | }} | ||
| 210. sor: | 225. sor: | ||
}} | }} | ||
[[Kategória: | [[Kategória:Villamosmérnök]] | ||
A lap jelenlegi, 2014. március 13., 14:59-kori változata
A 2014. január 7-i Infokommunikáció-vizsga feladatai és megoldásai. A 2. és 9. feladat három, a többi két pontot ér.
1. feladat
Adott egy kód, mely a 2 bites üzenetekből a következő kódszavakat álltja elő:
- 00: 00000
- 01: 01110
- 10: 10101
- 11: 11011
a) Adja meg a kód szisztematikus generátormátrixát! v=(01010) vett szó esetén melyik kódszó lett kiküldve a legnagyobb valószínűséggel?
k=2 (üzenethossz), n=5 (kódszóhossz)<br\> A G szisztematikus generátormátrix azon két kódszóból áll, melyeknek első 2-2 bitjéből egységmátrix alakítható ki. Az első két oszlop egy k-s egységmátrix, a harmadik-ötödik sorok pedig B mátrixot alkotják. <br\>
A 01110 kódszó csak 1 bitben tér el v-től, míg a többi több bitben, így valószínűleg ez lett kiküldve.b) Adja meg a paritásellenőrző mátrixot! A fenti v-re adja meg a szindrómát!
A paritásellenőrző mátrix B transzponáltjának és egy (n-k)-s egységmátrixnak egymás mellé rakásából alakul ki. <br\>
A szindróma:2. feladat
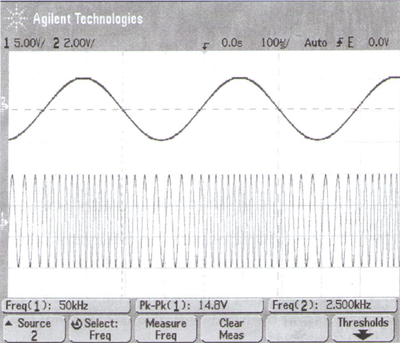 <br\><br\>
a) Frekvencia- vagy fázismodulált a képen látható jel? Miért?
<br\><br\>
a) Frekvencia- vagy fázismodulált a képen látható jel? Miért?
b) Becsülje meg a jel frekvencia- és fázislöketét!
a modulált jel alakja: ahol
Az oszcilloszkóp képről leolvasható adatok:
a moduláló jel amplitúdója
c) Milyen demodulátort javasolna? Rajzolja fel a blokkvázlatát!
3. feladat
Egy a 900 MHz-es sávban működő vevőantennával az interferenciazóna határán dolgozunk. Az antenna 5 m magasan van.<br\> a) Hány dB-vel változik a teljesítmény, ha a vevőantennánk magasságát felére csökkentjük?
Az interferenciazóna határán a szinusz argumentuma pontosan , tehát . Ha felére csökkentjük hr értékét, a szinusz argumentuma is feleződik.
A teljesítmény a térerősség négyzetével arányos, tehát az eredeti állapothoz képest feleződni fog, ami 3 dB-es csökkenést jelent.b) Hány dB-vel változik a teljesítmény, ha a vevőantennánk magasságát kétszeresére növeljük?
Az előbbi képletbe kétszeres hr-t helyettesítve a szinusz argumentuma lesz.
Nulla térerősség esetén a teljesítmény is 0 watt, ami dB-skálán . Bármekkora is volt tehát a kezdeti teljesítmény, az antenna magasságának kétszerezése után végtelen decibellel csökkent az értéke.4. feladat
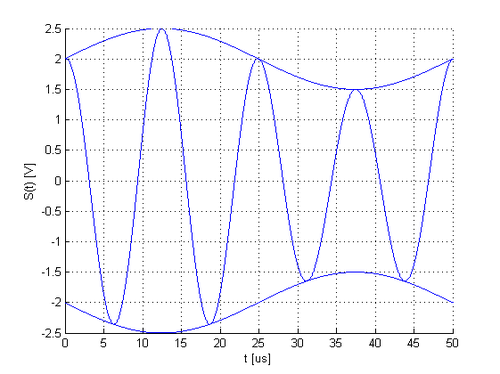
Egy AM-DSB modulált jel frekvenciája 80 kHz, a moduláló jel 20 kHz-es szinuszjel. A modulált jel csúcsértéke 2,5 V, a modulációs mélység 25%.<br\> a) Rajzolja fel a jel egy legalább 50 mikroszekundum hosszú szakaszát!
b) Írja fel a modulált jel időfüggvényét! Milyen mértékegységben kell beírni az idő értékét? Milyen frekvenciájú összetevői vannak a modulált jelnek, és mennyi ezek amplitúdója?
A frekvencia kHz-ben van megadva, az időt ezért ms-ban kell beírni.<br\> <br\> A jel komponensei és amplitúdójuk:
- 80 kHz : 2 V
- 80-20 = 60 kHz : 0,5/2=0,25 V
- 80+20 = 100 kHz : 0,5/2=0,25 V
5. feladat
Szuperheterodin vevő középfrekvenciája 10,7 MHz.<br\> a) Felső keverést alkalmazva hova kell hangolnunk a vevő oszcillátorát, hogy a 107 MHz-es frekvenciájú adót hallgassuk?
Felső keverés: , ahol Fv az adó frekvenciája.<br\>
b) Mekkora az előbbi adó tükörfrekvenciája?
6. feladat
Egy digitális rendszerben a bemenő és a visszaállító szűrő is ideális aluláteresztő jellegű, de sávszélességük nem egyezik meg. A bemenetre 1 kHz-es szimmetrikus négyszögjelet adunk, aminek minden páratlan felharmonikusa létezik az alapharmonikus mellett, de a kimeneten csak 1, 3, 7, 9 kHz-es komponensek jelennek meg.<br\> a) Mekkora lehetett a bemenő és a visszaállító szűrő sávszélessége?
- Nincs 5 kHz-es felharmonikus, de 3 kHz-es van, tehát a bemenő szűrő sávszélessége nagyobb, mint 3 kHz, de kisebb, mint 5 kHz.
- A legnagyobb komponens értéke 9 kHz, tehát a visszaállító szűrő sávszélessége nagyobb 9 kHz-nél.
b) A fenti adatok alapján adja meg a mintavételi frekvenciát!
7. feladat
a) Mi a fair queuing előnye a szigorú prioritáskezeléssel szemben?
b) Mi a WFQ algoritmus előnye a fair queuing-gal szemben?
8. feladat
Egy GSM-rendszerben MS-A1 és MS-A2 is az hálózat előfizetője, de MS-A2 a hálózatban roamingol.<br\> a)-b) ill. c)-d) együtt érnek 1-1 pontot<br\> a) MS-A1 hívja MS-A2-t. Melyik VLR kerül lekérdezésre a HLRα által?
b) Melyik MSC értesül erről?
c) Mely hálózati elemek értesülnek MS-A2 beszélgetés közbeni hálózaton belüli mozgásáról?
d) A hívás bontása után MS-A2 SMS-t ír MS-A1-nek, aki a tengerbe dobta készülékét. Melyik hálózati elem tárolja az SMS-t annak kézbesítéséig/lejártáig?
9. feladat
DVB-C rendszerben 64QAM helyett 256QAM-et használunk. 8 MHz-es a raszter, 33,3333%-os lekerekítésű emelt koszinuszos a spektrum.<br\> a) Mekkora a szimbólum- és a bitsebesség? Hány csatorna fér el a rendszerben, ha egy csatorna átlagos sávszélessége 1,5 Mbps?
<br\> Szimbólumsebesség: <br\> A 256QAM egy szimbólumban bitet visz át, a bitsebesség tehát <br\>
A rendszerben csatorna fér el.b) Mik a 6 Mbps sebességű kódoló használatának előnyei ill. hátrányai?
- Előny: a 6 Mbps-es csatornán jobb képminőséget lehet szolgáltatni (akár már HD-t is)
- Hátrány: több helyet foglal el egy csatorna -> kevesebb csatorna fér el egy raszterben
c) Mik az előnyei és hátrányai annak, ha 64QAM helyett 1024QAM-et használunk?
- Előny: 6 helyett 10 bit átvitele egy jelzési időn belül, nagyobb bitsebesség.
- Hátrány: nagyobb teljesítményigény, kisebb zajtűrés
10. feladat
a) A Kraft-egyenlőtlenség segítségével bizonyítsa be, hogy lehet-e egyértelműen megfejthető kódot készíteni a következő kódszóhosszakkal: 2,2,3,3,3,4,4,4,4!
Ha teljesül a Kraft-egyenlőtlenség: , ahol li az i-edik kódszó hossza, akkor lehet egyértelműen megfejthető kódot készíteni.
, tehát nem lehetséges.b) Készítsen prefixmentes kódot az alábbi kódszóhosszakkal: 2,2,3,3,3,5,5,5,5
Prefixmentes kód: egyik kódszó sem előtagja a másiknak. Jó megoldás például:
- 2 hosszúak:
- 00
- 11
- 3 hosszúak:
- 010
- 011
- 100
- 5 hosszúak:
- 10100
- 10101
- 10110
- 10111