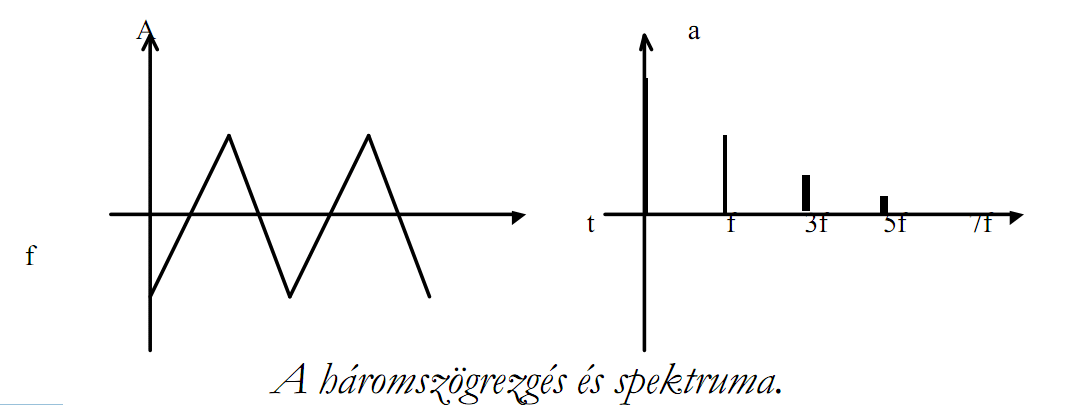„Laboratórium 1 - 2008 őszi ZH megoldások” változatai közötti eltérés
a David14 átnevezte a(z) Labor 1. 2008 ZH-k lapot a következő névre: Laboratórium 1 - 2008 őszi ZH megoldások |
a autoedit v2: fájlhivatkozások egységesítése, az új közvetlenül az adott fájlra mutat |
||
| (7 közbenső módosítás, amit 5 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
== 2008 őszi ZH == | |||
=== 1. Feladat === | |||
'''Egy 10 V csúcsértékű, 1 kHz frekvenciájú szimmetrikus négyszögjelet mérünk az alábbi műszerekkel, mekkora értéket mutatnak?''' | |||
Mindegyik szinuszos jelet feltételez, és mindegyik effektív értéket jelez ki. | |||
= | {| border="1" | ||
|'''Mérőműszer''' || '''Mért érték''' || '''Kijelzett érték''' | |||
|- | |||
|'''Effektív érték mérő''' || <math> 10 V </math> || <math> 10 V </math> | |||
| | |- | ||
|'''Csúcsértékmérő''' || <math> 10 V </math> || <math> \frac{10}{\sqrt{2}} V </math> | |||
| | |- | ||
|'''Abszolút középértékmérő''' || <math> 10 V </math> || <math> 10* \frac{\pi}{2\sqrt{2}} V </math> | |||
| | |||
|} | |} | ||
// | ''Nem biztos, hogy helyes ez a megoldás!'' | ||
Effektív és csúcsérték mérő fel volt cserélve, javítva. | |||
[http://bme.ysolt.net/4_felev/Merestechnika/Peceli_jegyzet/mt-ea-6.pdf Műszerek leírása (3. oldali táblázat)] | |||
=== 2. Feladat === | |||
'''Azonos frekvenciájú szinuszos jelek közötti fázisszöget mérünk oszcilloszkóppal időeltolódás és periódusidő alapján:''' | |||
'''a) Rajzolja fel a mérési elrendezést!''' | |||
A két jelet az oszcilloszkóp két különböző csatornájára tesszük. Mindkét jelen megkeresünk egy azonos fázishelyzetnek megfelelő értéket, célszerű a nullátmenetet választani. Ezek távolsága adja meg az időtengelyen a késleltetést, ami <math> \Delta t</math>. A T periódusidő meghatározható bármelyik jel két egymás utáni azonos irányú nullátmenete alapján. | |||
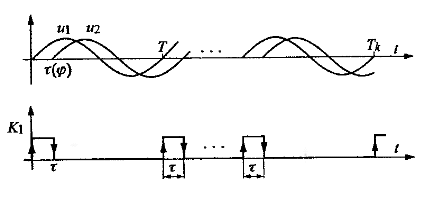
'''b) Rajzolja fel a mért jelalakokat, jelölje be rajta a mért mennyiségeket, és adja meg a fázisszög származtatási összefüggését!''' | |||
A fázisszög az alábbi képlettel határozható meg: <math> \varphi = 360^{\circ} \frac{\Delta t}{T} </math> | |||
[[File:Labor1 kép10.gif]] | |||
'''c) A periódusidőt és a fázistolást ugyanazzal az időalappal mérjük. A leolvasási bizonytalanság 1%, az időalap-generátor erősítéshibája 0,5% és a függőleges erősítő erősítőhibája 0,5%. Mekkora a fázisszögmérés relatív hibája legrosszabb esetben?''' | |||
A mérés előnye, hogy nem függ a pontosság az oszcilloszkóp időalapjának pontosságától. Legrosszabb esetben ( ''worst case'' ) a hiba: 1%, mivel az erősítéshiba nem változtatja meg a nullátmeneteket. [Hibás?] | |||
A | Másik lehetséges megoldás: két leolvasás történik, <math> \Delta t</math> és T bizonytalansága egyaránt 1%. A worst case összegzésnél a tényezők szerinti parciális deriválás és súlyozás után kijön, hogy a relatív hibához a kitevőjük (1 és -1) abszolút értékével járulnak hozzá, azaz '''2% lesz a bizonytalanság'''.--[[Szerkesztő:Mp9k1|Mp9k1]] ([[Szerkesztővita:Mp9k1|vita]]) 2013. december 5., 23:22 (UTC) | ||
=== 3. Feladat === | |||
'''Adja meg az ideális szinuszjel és szimmetrikus háromszögjel amplitúdóspektrumát! A spektrumokat jellegre helyes ábrán szemléltesse!''' | |||
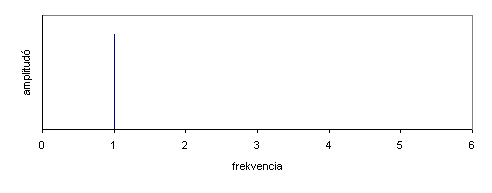
*Szinusz jel spektruma: | |||
[[File:Labor1 kép11.gif]] | |||
*Háromszögjel időfüggvénye és spektruma: | |||
[[File:Labor1 kép12.gif]] | |||
* | *Megjegyzés: spektrum meghatározása: <math> a_n = \frac{4A}{n^2 {\pi}^2} \sin \left| \frac{n \pi}{2} \right| </math> | ||
=== 4. Feladat === | |||
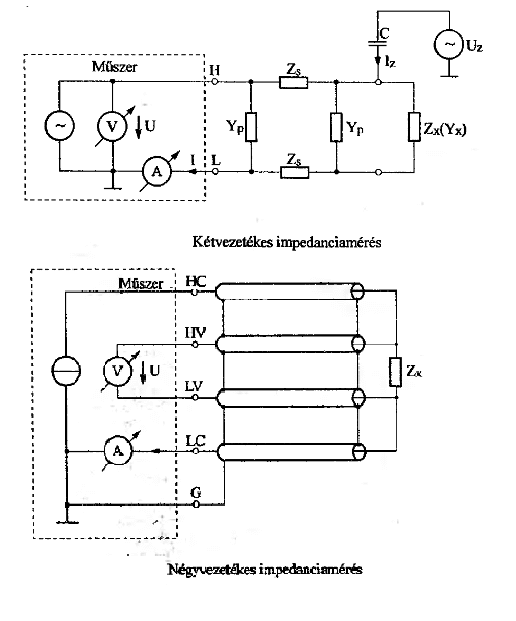
'''Rajzolja föl a kettő- illetve a négyvezetékes impedanciamérést! Milyen esetekben fontos a négyvezetékes elrendezés?''' | |||
Négyvezetékes mérés jelentősége: Kis impedanciák esetén a hozzávezetési és kontaktellenállásokat hatástalanítandó, a négykapcsú mérési elrendezés indokolt, ha összemérhető a mérendő ellenállás értéke a hozzávezetések ellenállásával. | |||
[[File:Labor1 kép13.gif]] | |||
=== 5. Feladat === | |||
'''Rajzolja fel egy 2:1 áttételű transzformátor modelljét! Ismertesse a modell fizikai jelentését! Hogyan viszonyulnak egymáshoz a modellparaméterek laza és szoros csatolás esetén?''' | |||
[[File:Labor1 kép14.gif]] | |||
{| border="1" | |||
| | | <math> U_1 </math> || primer feszültség || | ||
|- | |||
| | | <math> U_2 </math> || szekunder feszültség || | ||
|- | |||
| | | <math> Z_1, Z_2 </math> || primer, szekunder oldali szórási impedanciák || Valós komponens: rézellenállás; Képzetes komponens: szórási induktivitás | ||
|- | |||
| <math> Z_0 </math> || mágnesező impedancia || <math> L_0 </math> mágnesező impedanciából és <math> R_0 </math> vasveszteségi ellenállásból áll | |||
|} | |} | ||
Szorosnál a főmező reaktancia nagyságrendekkel nagyobb, mint a szórt, lazánál pedig fordítva. | |||
=== 6. Feladat === | |||
'''Egy D flip-flopot a következő gyári adatok jellemeznek:''' | |||
{| border="1" | {| border="1" | ||
| 80. sor: | 92. sor: | ||
|} | |} | ||
A flip-flop adatbemenetére jutó jelet egy inverteren keresztül vezetjük keresztül az alábbi ábrán látható módon. | '''A flip-flop adatbemenetére jutó jelet egy inverteren keresztül vezetjük keresztül az alábbi ábrán látható módon.''' | ||
[[File:Labor1 kép15.gif]] | |||
Az inverter jelterjedési késleltetései: | '''Az inverter jelterjedési késleltetései:''' | ||
{| border="1" | {| border="1" | ||
| 94. sor: | 106. sor: | ||
|} | |} | ||
'''Adja meg a worst case setup időt erre a módosított flip-flopra!''' | |||
15 ns a setup worst case-ben | |||
<math> t_{su}' = t_{su} - min(t_{LH}) + max(t_{LH},t_{HL}) </math> | <math> t_{su}' = t_{su} - min(t_{LH}) + max(t_{LH},t_{HL}) </math> | ||
| 102. sor: | 114. sor: | ||
<math> t_h' = t_h + max(t_{LH}) - min(t_{LH},t_{HL}) </math> | <math> t_h' = t_h + max(t_{LH}) - min(t_{LH},t_{HL}) </math> | ||
Itt a '-s tagok a módosított ff paraméterei. | Itt a '-s tagok a módosított ff paraméterei. Az első korrekciós tag az órajel késleltetésének a hatása, ezért kell csak a <math> t_{LH} </math> sorból venni a min/max értékeket (táblázat első sora). A második korrekciós tag az adat késleltetésének eredménye, így a <math> t_{LH} </math> és <math> t_{HL} </math> sorokat is figyelembe kell venni (tehát az egész táblázatot). | ||
Az első korrekciós tag az órajel késleltetésének a hatása, ezért kell csak a <math> t_{LH} </math> sorból venni a min/max értékeket (táblázat első sora). | |||
A második korrekciós tag az adat késleltetésének eredménye, így a <math> t_{LH} </math> és <math> t_{HL} </math> sorokat is figyelembe kell venni (tehát az egész táblázatot). | |||
Amikor egy korrekciós taggal növeljük az eredményt, akkor maximim kell, amikor csökkentjük, akkor minimum kell, így lesz a végeredmény maximális, tehát worst-case eredmény". | Amikor egy korrekciós taggal növeljük az eredményt, akkor maximim kell, amikor csökkentjük, akkor minimum kell, így lesz a végeredmény maximális, tehát worst-case eredmény". | ||
=== 7. Feladat === | |||
'''Rajzolja fel a bipoláris tranzisztor 5 elemes helyettesítőképét! Adja meg a helyettesítőkép elemeit a tranzisztor fizikai paramétereivel!''' | |||
[[File:Labor1 kép16.gif]] | |||
* <math> g_{b'c} = \frac{1}{r_c}- \mu g_{b'e} </math> | * <math> g_{b'c} = \frac{1}{r_c}- \mu g_{b'e} </math> | ||
| 118. sor: | 130. sor: | ||
* <math> g_m = \frac{ I_c }{ U_t } </math> | * <math> g_m = \frac{ I_c }{ U_t } </math> | ||
=== 8. Feladat === | |||
'''Egy törölhető 6-os számláló (<math> Q_2 \dots Q_0, Cl, CLK </math>) a katalógus alapján maximálisan 30MHz-es órajellel működtethető. Meg kell határoznunk, hogy egy konkrét példánynak mekkora a maximális működési frekvenciája. Rendelkezésre áll egy változtatható frekvenciájú (1Hz...200MHz) generátor és egy logikai analizátor. A számláló bemeneteire tetszőleges konstans logikai értéket kapcsolhat (kapcsolók segítségével). Röviden írja le, hogy miként oldaná meg a feladatot!''' | |||
A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. A végállapotot (111) állítjuk be leállási feltételként. 30MHz-től növekvő frekvenciákon ellenőrizzük, hogy a számláló egymást követő állapotai megfelelnek-e a bináris számláló működésének. A legalacsonyabb olyan frekvencia ahol még igen a maximális működési frekvencia. | A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. A végállapotot (111) állítjuk be leállási feltételként. 30MHz-től növekvő frekvenciákon ellenőrizzük, hogy a számláló egymást követő állapotai megfelelnek-e a bináris számláló működésének. A legalacsonyabb olyan frekvencia ahol még igen a maximális működési frekvencia. | ||
| 125. sor: | 138. sor: | ||
A ''Clear'' -re triggerelünk és az analízist az fogja indítani, hogy töröljük az értékeket. | A ''Clear'' -re triggerelünk és az analízist az fogja indítani, hogy töröljük az értékeket. | ||
=== 9. Feladat === | |||
'''Hasonlítsa össze a párhuzamos port mérésben vizsgált két üzemmódjának (SPP és EPP) paramétereit az alábbi kategóriák szerint! Amennyiben egy állítás az adott üzemmódra nézve igaz "+", ha hamis akkor "-" jellel jelölje!''' | |||
{| border="1" | {| border="1" | ||
| 141. sor: | 156. sor: | ||
|} | |} | ||
=== 10. Feladat === | |||
'''Adjon meg egy olyan tesztvektor-sorozatot az alábbi állapottáblával megadott, egyetlen X bemenettel rendelkező automatához, amely leteszteli az összes állapotátmenetét. A mellékelt táblázatban azt is tüntesse fel, hogy adott bemenetre milyen állapotba kerül az automata! Az automata a RESET jelre az A állapotba kerül.''' | |||
{| border="1" | {| border="1" | ||
| 153. sor: | 170. sor: | ||
|} | |} | ||
A -> B | Átmenetek: | ||
B -> C,A | *A -> B | ||
C -> C,A | *B -> C,A | ||
*C -> C,A | |||
{| border="1" | {| border="1" | ||
| 166. sor: | 185. sor: | ||
|} | |} | ||
====1. | == 2008 őszi pótZH == | ||
=== 1. Feladat === | |||
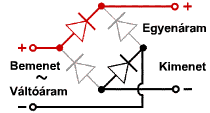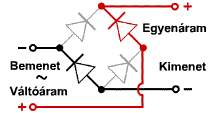
'''Graetz típusú egyenirányító:''' | |||
'''a) Jelölje a váltakozó áramú bemenetet és az egyenáramú kimenetet, jelölje a polaritást is!''' | |||
'''b) Rajzolja fel a kimeneten megjelenő jel alakját abban az esetben, ha a bemenetre <math> f_0 </math> frekvenciájú szinuszos feszültséget kapcsolunk!''' | |||
A transzfer karakterisztika segítségével megrajzolható, hogy milyen a kimenet. | A transzfer karakterisztika segítségével megrajzolható, hogy milyen a kimenet. | ||
'''c) Adja meg az egyenirányított jel váltakozó komponensének frekvenciáját!''' | |||
A lüktető egyenáram frekvenciája a váltóáram duplája. | A lüktető egyenáram frekvenciája a váltóáram duplája. | ||
[[File:Labor1 kép17.gif]] | |||
[[File:Labor1 kép18.gif]] | |||
=== 2. Feladat === | |||
'''Ugyanaz mint az előzőben (azonos frekvenciájú szinuszos...)''' | |||
=== 3. Feladat === | |||
'''Adja meg a szimmetrikus négyszögjel amplitúdóspektrumát! Hogyan változik a spektrum, ha a szimmetria megsérül (az előjelváltás nem pontosan félperiódusonként következik be)? A spektrumot jellegre helyes ábrán szemléltesse!''' | |||
A spektrum: <math>f_0</math> frekvenciájú négyszögjel összetevői <math> n \cdot f_0 </math> frekvenciákon vannak, ahol <math> n </math> páratlan szám. Az egyes összetevők amplitúdói a frekvencia növekedtével <math> \frac{1}{x} </math> szerint csökkennek. | A spektrum: <math>f_0</math> frekvenciájú négyszögjel összetevői <math> n \cdot f_0 </math> frekvenciákon vannak, ahol <math> n </math> páratlan szám. Az egyes összetevők amplitúdói a frekvencia növekedtével <math> \frac{1}{x} </math> szerint csökkennek. | ||
Az alapfrekvencia páratlanszámú többszörösein jelennek meg összetevők csökkenő amplitúdóval, azaz | Az alapfrekvencia páratlanszámú többszörösein jelennek meg összetevők csökkenő amplitúdóval, azaz f frekvenciájú négyszögjelnek lesz összetevője <math> f, 3f, 5f, 7f ... </math> frekvenciákon, ez a végtelenig tart elméletileg. (ugyanis a négyszögjel végtelen sok ilyen szinuszból állítható elő tökéletesen) | ||
Ha nem szimmetrikus a négyszögjel, akkor megjelennek a páros számú többszörösei is az alapharmonikusnak. | Ha nem szimmetrikus a négyszögjel, akkor megjelennek a páros számú többszörösei is az alapharmonikusnak. | ||
=== 4. Feladat === | |||
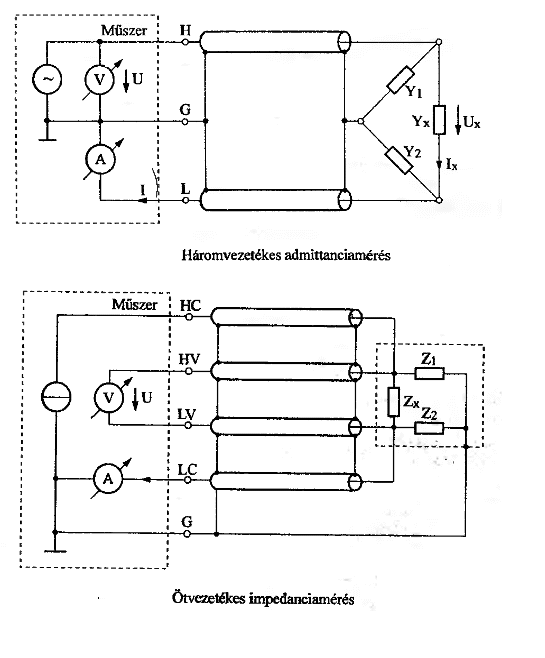
'''Három és ötvezetékes mérés. Milyen esetekben fontos az ötvezetékes?''' | |||
[[File:Labor1 kép19.gif]] | |||
Hárompólus négykapcsú mérésénél ötvezetékes mérést kell használnunk, <math> Z_1, Z_2 </math> impedanciák áramát G pontba tereljük. | Hárompólus négykapcsú mérésénél ötvezetékes mérést kell használnunk, <math> Z_1, Z_2 </math> impedanciák áramát G pontba tereljük. | ||
=== 5. Feladat === | |||
'''Egy 600 <math> \Omega </math> -os forrást TELECOM transzformátor segítségével 600 <math> \Omega </math> -os terheléshez illesztünk. A transzformátor primer és szekunder ellenállása 25,3 <math> \Omega </math>. Számítsa ki a transzformátor áttételét!''' | |||
<math> R_b = R_1 + n^{2}R2 + n^{2}R_t </math> | Képlet: <math> R_b = R_1 + n^{2}R2 + n^{2}R_t </math> ahol: | ||
*<math> R_b </math> - generátor belső ellenállása | |||
<math> R_b </math> - generátor belső ellenállása | *<math> R_1, R_2 </math> - tekercsek DC ellenállása | ||
<math> R_1, R_2 </math> - tekercsek DC ellenállása | *<math> R_t </math> - terhelő ellenállás | ||
<math> R_t </math> - terhelő ellenállás | *<math> n </math> - menetszám áttétel n = <math> \frac{N_{primer}}{N_{szekunder}} </math> | ||
<math> n </math> - menetszám áttétel n = <math> \frac{N_{primer}}{N_{szekunder}} </math> | |||
<math> n=\sqrt{\frac{R_b - R_1}{R_2 + R_t}}=0.95 </math> | Tehát: <math> n=\sqrt{\frac{R_b - R_1}{R_2 + R_t}}=0.95 </math> | ||
=== 6. Feladat === | |||
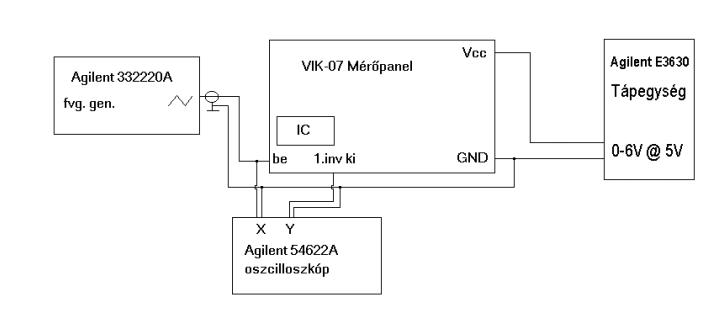
'''TTL inverter transzfer karakterisztikájának mérés:''' | |||
*'''Rajzolja fel a mérési elrendezést''' | |||
*'''Határozza meg milyen gerjesztést alkalmazna''' | |||
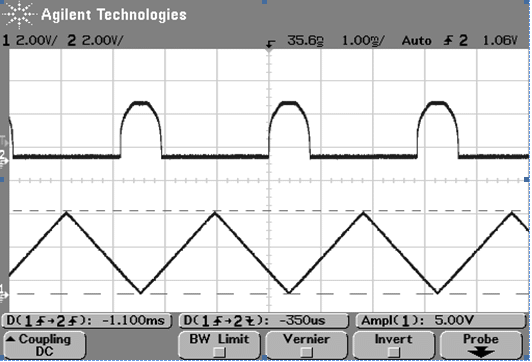
*'''Ábrázolja a gerjesztő jel és az inverter arra adott válaszának időfüggvényét egy ábrán. Ne feledkezzen meg az _y_ tengely (feszültség) helyes skálázásáról!''' | |||
[[File:Labor1 kép20.gif]] | |||
< | A mérésen 0V alapszintű 5 <math>V_pp</math> nagyságú kb. 350Hz-es jellel kellett vizsgálni XY üzemmódban (mindképpen pozitív feszültség kell, hiszen a TTL áramkörök a negatív feszültséget levágják) | ||
[[File:Labor1 kép21.gif]] | |||
=== 7. Feladat === | |||
'''Rajzolja fel a bipoláris tranzisztor h21 paraméterének mérésére szolgáló mérési összeállítást! Röviden ismertesse a mérés lépéseit!''' | |||
<math> h_{21} = \frac{\Delta I_c}{\Delta I_B} | U_{CE}=konstans </math> | <math> h_{21} = \frac{\Delta I_c}{\Delta I_B} | U_{CE}=konstans </math> | ||
| 233. sor: | 262. sor: | ||
Közös emitteres kapcsolás, áramgenerátorosan meghajtjuk a bázis felől (feszgenerátor, és a bemeneti ellenálláshoz képest sokkal nagyobb ellenállás) és UCE=állandó az a kimeneti ellenálláshoz képest rövidzár (gyakorlatilag árammérő-vel kell lezárni). <math> I_B, I_C </math> értékéből számítható. | Közös emitteres kapcsolás, áramgenerátorosan meghajtjuk a bázis felől (feszgenerátor, és a bemeneti ellenálláshoz képest sokkal nagyobb ellenállás) és UCE=állandó az a kimeneti ellenálláshoz képest rövidzár (gyakorlatilag árammérő-vel kell lezárni). <math> I_B, I_C </math> értékéből számítható. | ||
Itt van elrendezés: | Itt van elrendezés: [[Laboratórium 1 - 2006 őszi ZH megoldások]] | ||
=== 8. Feladat === | |||
'''Egy ciklikusan működő állapotgép 2MHz-es órajellel működik. Az állapotgép 3 bites állapotai: 100, 010, 001. A többi kód nem fordulhat elő. Logikai analizátorral hogyan ellenőrizné, hogy nem lép hibás kódú állapotba a hálózat?''' | |||
A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. 2MHz-en ellenőrizzük, hogy a számláló állapotai megfelelnek-e az állapotgép működésének. | A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. 2MHz-en ellenőrizzük, hogy a számláló állapotai megfelelnek-e az állapotgép működésének. | ||
=== 9. Feladat === | |||
'''Neptun kód átvitele 2 Stopbittel:''' | |||
* Neptun kód: 6 karakter | * Neptun kód: 6 karakter | ||
| 257. sor: | 290. sor: | ||
|} | |} | ||
=== 10. Feladat === | |||
'''Hogyan tesztelne le egy FPGA-ban megvalósított, viszonylag kevés állípotú szinkron sorrendi hálózatot, ha a logikai analizátor áll rendelkezésre és az FPGA-ban még sok erőforrás van kihasználatlanul (bőven van hely további hardver megvalósításához)?''' | |||
[[ | [[Kategória:Villamosmérnök]] | ||
A lap jelenlegi, 2017. július 12., 14:36-kori változata
2008 őszi ZH
1. Feladat
Egy 10 V csúcsértékű, 1 kHz frekvenciájú szimmetrikus négyszögjelet mérünk az alábbi műszerekkel, mekkora értéket mutatnak?
Mindegyik szinuszos jelet feltételez, és mindegyik effektív értéket jelez ki.
| Mérőműszer | Mért érték | Kijelzett érték |
| Effektív érték mérő | ||
| Csúcsértékmérő | ||
| Abszolút középértékmérő |
Nem biztos, hogy helyes ez a megoldás! Effektív és csúcsérték mérő fel volt cserélve, javítva.
Műszerek leírása (3. oldali táblázat)
2. Feladat
Azonos frekvenciájú szinuszos jelek közötti fázisszöget mérünk oszcilloszkóppal időeltolódás és periódusidő alapján:
a) Rajzolja fel a mérési elrendezést!
A két jelet az oszcilloszkóp két különböző csatornájára tesszük. Mindkét jelen megkeresünk egy azonos fázishelyzetnek megfelelő értéket, célszerű a nullátmenetet választani. Ezek távolsága adja meg az időtengelyen a késleltetést, ami . A T periódusidő meghatározható bármelyik jel két egymás utáni azonos irányú nullátmenete alapján.
b) Rajzolja fel a mért jelalakokat, jelölje be rajta a mért mennyiségeket, és adja meg a fázisszög származtatási összefüggését!
A fázisszög az alábbi képlettel határozható meg:
c) A periódusidőt és a fázistolást ugyanazzal az időalappal mérjük. A leolvasási bizonytalanság 1%, az időalap-generátor erősítéshibája 0,5% és a függőleges erősítő erősítőhibája 0,5%. Mekkora a fázisszögmérés relatív hibája legrosszabb esetben?
A mérés előnye, hogy nem függ a pontosság az oszcilloszkóp időalapjának pontosságától. Legrosszabb esetben ( worst case ) a hiba: 1%, mivel az erősítéshiba nem változtatja meg a nullátmeneteket. [Hibás?]
Másik lehetséges megoldás: két leolvasás történik, és T bizonytalansága egyaránt 1%. A worst case összegzésnél a tényezők szerinti parciális deriválás és súlyozás után kijön, hogy a relatív hibához a kitevőjük (1 és -1) abszolút értékével járulnak hozzá, azaz 2% lesz a bizonytalanság.--Mp9k1 (vita) 2013. december 5., 23:22 (UTC)
3. Feladat
Adja meg az ideális szinuszjel és szimmetrikus háromszögjel amplitúdóspektrumát! A spektrumokat jellegre helyes ábrán szemléltesse!
- Szinusz jel spektruma:
- Háromszögjel időfüggvénye és spektruma:
- Megjegyzés: spektrum meghatározása:
4. Feladat
Rajzolja föl a kettő- illetve a négyvezetékes impedanciamérést! Milyen esetekben fontos a négyvezetékes elrendezés?
Négyvezetékes mérés jelentősége: Kis impedanciák esetén a hozzávezetési és kontaktellenállásokat hatástalanítandó, a négykapcsú mérési elrendezés indokolt, ha összemérhető a mérendő ellenállás értéke a hozzávezetések ellenállásával.
5. Feladat
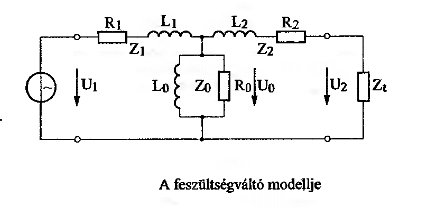
Rajzolja fel egy 2:1 áttételű transzformátor modelljét! Ismertesse a modell fizikai jelentését! Hogyan viszonyulnak egymáshoz a modellparaméterek laza és szoros csatolás esetén?
| primer feszültség | ||
| szekunder feszültség | ||
| primer, szekunder oldali szórási impedanciák | Valós komponens: rézellenállás; Képzetes komponens: szórási induktivitás | |
| mágnesező impedancia | mágnesező impedanciából és vasveszteségi ellenállásból áll |
Szorosnál a főmező reaktancia nagyságrendekkel nagyobb, mint a szórt, lazánál pedig fordítva.
6. Feladat
Egy D flip-flopot a következő gyári adatok jellemeznek:
| setup time | 10 ns | |
| hold time | 5 ns |
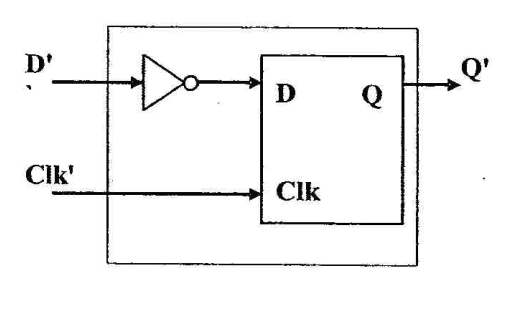
A flip-flop adatbemenetére jutó jelet egy inverteren keresztül vezetjük keresztül az alábbi ábrán látható módon.
Az inverter jelterjedési késleltetései:
| min | max | |
| 3ns | 5ns | |
| 2ns | 4ns |
Adja meg a worst case setup időt erre a módosított flip-flopra!
15 ns a setup worst case-ben
Itt a '-s tagok a módosított ff paraméterei. Az első korrekciós tag az órajel késleltetésének a hatása, ezért kell csak a sorból venni a min/max értékeket (táblázat első sora). A második korrekciós tag az adat késleltetésének eredménye, így a és sorokat is figyelembe kell venni (tehát az egész táblázatot).
Amikor egy korrekciós taggal növeljük az eredményt, akkor maximim kell, amikor csökkentjük, akkor minimum kell, így lesz a végeredmény maximális, tehát worst-case eredmény".
7. Feladat
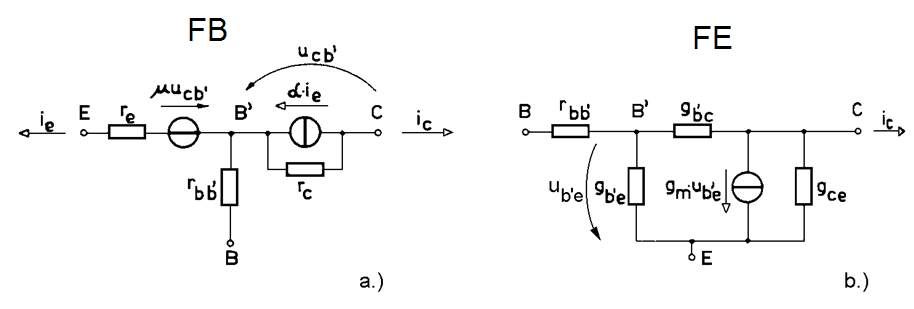
Rajzolja fel a bipoláris tranzisztor 5 elemes helyettesítőképét! Adja meg a helyettesítőkép elemeit a tranzisztor fizikai paramétereivel!
8. Feladat
Egy törölhető 6-os számláló () a katalógus alapján maximálisan 30MHz-es órajellel működtethető. Meg kell határoznunk, hogy egy konkrét példánynak mekkora a maximális működési frekvenciája. Rendelkezésre áll egy változtatható frekvenciájú (1Hz...200MHz) generátor és egy logikai analizátor. A számláló bemeneteire tetszőleges konstans logikai értéket kapcsolhat (kapcsolók segítségével). Röviden írja le, hogy miként oldaná meg a feladatot!
A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. A végállapotot (111) állítjuk be leállási feltételként. 30MHz-től növekvő frekvenciákon ellenőrizzük, hogy a számláló egymást követő állapotai megfelelnek-e a bináris számláló működésének. A legalacsonyabb olyan frekvencia ahol még igen a maximális működési frekvencia.
A Clear -re triggerelünk és az analízist az fogja indítani, hogy töröljük az értékeket.
9. Feladat
Hasonlítsa össze a párhuzamos port mérésben vizsgált két üzemmódjának (SPP és EPP) paramétereit az alábbi kategóriák szerint! Amennyiben egy állítás az adott üzemmódra nézve igaz "+", ha hamis akkor "-" jellel jelölje!
| Tulajdonság | SPP | EPP | Magyarázat ( ez nem volt feladat ) |
| Kétirányú adatátvitel | - | + | Az SPP módban csak kimenő irányú adatátvitel történik, EPP módban lehetséges a cím és adat kivitel mellett ezen paraméterek visszaolvasása is. |
| Nincs címzési lehetőség | + | - | Az SPP módhoz egyetlen 8 bites kimeneti adatregiszter tartozik. Az EPP módhoz egy 8 bites címregiszter és a lehetséges 256 egyedileg címezhető adat regiszterből csak az első 4 címhez tartozik egy-egy írható/olvasható 8 bites adatregiszter. |
| Nagy sebesség | ?+? | ||
| Átvitelszinkronizáció lehetősége | ?+? | ||
| Szoftveres átvitelvezérlés a PC-ben | + |
10. Feladat
Adjon meg egy olyan tesztvektor-sorozatot az alábbi állapottáblával megadott, egyetlen X bemenettel rendelkező automatához, amely leteszteli az összes állapotátmenetét. A mellékelt táblázatban azt is tüntesse fel, hogy adott bemenetre milyen állapotba kerül az automata! Az automata a RESET jelre az A állapotba kerül.
| X | 0 | 1 |
| A | B\0 | B\0 |
| B | C\1 | A\1 |
| C | C\1 | A\0 |
Átmenetek:
- A -> B
- B -> C,A
- C -> C,A
| RESET | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| X | - | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| állapot | A | B | A | B | C | C | A | B |
2008 őszi pótZH
1. Feladat
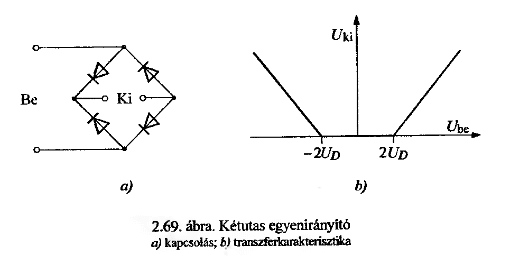
Graetz típusú egyenirányító:
a) Jelölje a váltakozó áramú bemenetet és az egyenáramú kimenetet, jelölje a polaritást is!
b) Rajzolja fel a kimeneten megjelenő jel alakját abban az esetben, ha a bemenetre frekvenciájú szinuszos feszültséget kapcsolunk!
A transzfer karakterisztika segítségével megrajzolható, hogy milyen a kimenet.
c) Adja meg az egyenirányított jel váltakozó komponensének frekvenciáját!
A lüktető egyenáram frekvenciája a váltóáram duplája.
2. Feladat
Ugyanaz mint az előzőben (azonos frekvenciájú szinuszos...)
3. Feladat
Adja meg a szimmetrikus négyszögjel amplitúdóspektrumát! Hogyan változik a spektrum, ha a szimmetria megsérül (az előjelváltás nem pontosan félperiódusonként következik be)? A spektrumot jellegre helyes ábrán szemléltesse!
A spektrum: frekvenciájú négyszögjel összetevői frekvenciákon vannak, ahol páratlan szám. Az egyes összetevők amplitúdói a frekvencia növekedtével szerint csökkennek.
Az alapfrekvencia páratlanszámú többszörösein jelennek meg összetevők csökkenő amplitúdóval, azaz f frekvenciájú négyszögjelnek lesz összetevője frekvenciákon, ez a végtelenig tart elméletileg. (ugyanis a négyszögjel végtelen sok ilyen szinuszból állítható elő tökéletesen)
Ha nem szimmetrikus a négyszögjel, akkor megjelennek a páros számú többszörösei is az alapharmonikusnak.
4. Feladat
Három és ötvezetékes mérés. Milyen esetekben fontos az ötvezetékes?
Hárompólus négykapcsú mérésénél ötvezetékes mérést kell használnunk, impedanciák áramát G pontba tereljük.
5. Feladat
Egy 600 -os forrást TELECOM transzformátor segítségével 600 -os terheléshez illesztünk. A transzformátor primer és szekunder ellenállása 25,3 . Számítsa ki a transzformátor áttételét!
Képlet: ahol:
- - generátor belső ellenállása
- - tekercsek DC ellenállása
- - terhelő ellenállás
- - menetszám áttétel n =
Tehát:
6. Feladat
TTL inverter transzfer karakterisztikájának mérés:
- Rajzolja fel a mérési elrendezést
- Határozza meg milyen gerjesztést alkalmazna
- Ábrázolja a gerjesztő jel és az inverter arra adott válaszának időfüggvényét egy ábrán. Ne feledkezzen meg az _y_ tengely (feszültség) helyes skálázásáról!
A mérésen 0V alapszintű 5 nagyságú kb. 350Hz-es jellel kellett vizsgálni XY üzemmódban (mindképpen pozitív feszültség kell, hiszen a TTL áramkörök a negatív feszültséget levágják)
7. Feladat
Rajzolja fel a bipoláris tranzisztor h21 paraméterének mérésére szolgáló mérési összeállítást! Röviden ismertesse a mérés lépéseit!
Közös emitteres kapcsolás, áramgenerátorosan meghajtjuk a bázis felől (feszgenerátor, és a bemeneti ellenálláshoz képest sokkal nagyobb ellenállás) és UCE=állandó az a kimeneti ellenálláshoz képest rövidzár (gyakorlatilag árammérő-vel kell lezárni). értékéből számítható.
Itt van elrendezés: Laboratórium 1 - 2006 őszi ZH megoldások
8. Feladat
Egy ciklikusan működő állapotgép 2MHz-es órajellel működik. Az állapotgép 3 bites állapotai: 100, 010, 001. A többi kód nem fordulhat elő. Logikai analizátorral hogyan ellenőrizné, hogy nem lép hibás kódú állapotba a hálózat?
A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. 2MHz-en ellenőrizzük, hogy a számláló állapotai megfelelnek-e az állapotgép működésének.
9. Feladat
Neptun kód átvitele 2 Stopbittel:
- Neptun kód: 6 karakter
- 1 karakter átvitele: 1 start bit + 8 adatbit(maga a karakter) + 2 stop bit (paritás nem volt megadva az +1 bit lenne még.)
- Tehát 1 karakter átvitele 11bit küldésével történik, innen 6 karakter = 66 bit
| 4-féle átviteli sebesség(gondolom) | számolás | neptun kód átviteléhez szükséges idő: |
| 19200 bps | 66/19200 | 0.00343 sec |
| 38400 bps | 66/38400 | 0.00171 sec |
| 57600 bps | 66/57600 | 0.00114 sec |
| 115200 bps | 66/115200 | 0.00057 sec |
10. Feladat
Hogyan tesztelne le egy FPGA-ban megvalósított, viszonylag kevés állípotú szinkron sorrendi hálózatot, ha a logikai analizátor áll rendelkezésre és az FPGA-ban még sok erőforrás van kihasználatlanul (bőven van hely további hardver megvalósításához)?