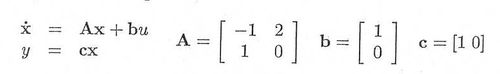„Laboratórium 2 - ZH, 2004 tavasz” változatai közötti eltérés
| (9 közbenső módosítás, amit 4 másik szerkesztő végzett, nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
[[File:Labor2_ZH_2004_ábra1.jpg|400px]] | [[File:Labor2_ZH_2004_ábra1.jpg|400px]] | ||
Az elemek értékei: C = 68 nF, R1 = 16 kOhm, R2 = 190 kOhm, | Az elemek értékei: C = 68 nF, R1 = 16 kOhm, R2 = 190 kOhm, R3 = 18 kOhm | ||
Határozza meg a kapcsolás feszültségerősítését 10 kHz-es bemenőfeszültség esetén! | Határozza meg a kapcsolás feszültségerősítését 10 kHz-es bemenőfeszültség esetén! | ||
| 265. sor: | 265. sor: | ||
[[File:Labor2_ZH_2004_ábra5.jpg| | [[File:Labor2_ZH_2004_ábra5.jpg|500px]] | ||
}} | }} | ||
| 287. sor: | 287. sor: | ||
}} | }} | ||
==10.== | ==10. Állapotteres szabályozás== | ||
Adott egy folytonos idejű szakasz állapotteres leírása: | Adott egy folytonos idejű szakasz állapotteres leírása: | ||
[[File:Labor2_ZH_2004_ábra7.jpg|500px]] | |||
A szakaszt <math>u=-Kx</math> állapot-visszacsatolással kompenzáljuk, ahol K = [2 4]. Adja meg a szakasz és a zárt szabályozási kör sajátértékeit (pólusait)! Stabil-e a szakasz, illetve a zárt rendszer? | |||
{{Rejtett | |||
|mutatott='''Megoldás''' | |||
|szöveg= | |||
A | A szakasz karakterisztikus egyenlete: | ||
<math> \varphi (s) = det [sI-A] = \left[ \begin{array}{cc} s+1 & -2 \\ -1 & s \end{array} \right]</math> <math>= s^2+s-2=(s-1)\cdot(s+2)=0 </math> | |||
<math> \varphi (s) = det [sI-A] = \left[ \begin{array}{cc} s+1 & -2 \\ -1 & s \end{array} \right]</math> <math>= s^2+s-2=(s-1)(s+2)=0 </math> | |||
Melynek gyökei a szakasz pólusai (sajátértékek), azaz <math>s_1=1</math> és <math>s_2=-2</math>. Mivel <math>s_1</math> valós része pozitív, ezért a szakasz instabil. | |||
<math> | A zárt rendszer állapotegyenlete <math>u=-Kx</math> behelyettesítés után: | ||
<math> \dot{x}=(A-B K)\cdot x </math> | |||
<math> y= C \cdot x </math> | <math> y= C \cdot x </math> | ||
<math> (A-BK)= \left[ \begin{array}{cc} -3 & -2 \\ -1 & | A zárt rendszer sajátértékeit az (A-BK) mátrix sajátértékei adják: | ||
<math> (A-BK)= \left[ \begin{array}{cc} -3 & -2 \\ 1 & 0 \end{array} \right] </math> | |||
<math> \varphi_c(s) = det[sI-(A-B K)] = \left[ \begin{array}{cc} s+3 & 2 \\ -1 & s \end{array} \right] =s^2+3s+2=(s+1)(s+2) </math>. | |||
Azaz a pólusok -1 és -2, melyek negatív valós résszel rendelkeznek, így a rendszer stabil. | Azaz a pólusok -1 és -2, melyek negatív valós résszel rendelkeznek, így a rendszer stabil. | ||
==11.== | |||
}} | |||
==11. Hőmérséklet-szabályozás== | |||
Vázolja fel a digitális hőmérséklet-szabályozási kör blokkvázlatát! Tüntesse fel a jelek elnevezését, jellegét és dimenzióját! | Vázolja fel a digitális hőmérséklet-szabályozási kör blokkvázlatát! Tüntesse fel a jelek elnevezését, jellegét és dimenzióját! | ||
{{Rejtett | |||
|mutatott='''Megoldás''' | |||
|szöveg= | |||
[[File:Labor2_ZH_2014_ábra8.JPG|600px]] | |||
A jelek elnevezései és dimenziói: | |||
*<math>r</math> - Alapjel <math>[C^{\circ}]</math> | |||
*<math>u</math> - Vezérlőjel <math>[V]</math> | |||
*<math>u_{k}</math> - Korlátozott vezérlőjel <math>[V]</math> | |||
*<math>\vartheta</math> - Hőmérséklet <math>[C^{\circ}]</math> | |||
}} | |||
[[Kategória:Villamosmérnök]] | |||
A lap jelenlegi, 2016. május 9., 14:11-kori változata
1. Erősítő kapcsolás
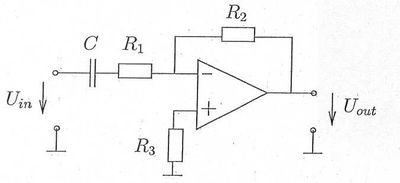
Adott az alábbi kapcsolás:
Az elemek értékei: C = 68 nF, R1 = 16 kOhm, R2 = 190 kOhm, R3 = 18 kOhm
Határozza meg a kapcsolás feszültségerősítését 10 kHz-es bemenőfeszültség esetén!
Határozza meg R3 optimális értékét!
2. NYÁK tervezés
A NYÁK-tervező programok milyen nézetben (alul/felül) ábrázolják a NYÁK-rétegeket? (A legalsó réteget honnan látja a tervező: felülről, a felső réteg felől, vagy alulról?)
Mi a Gerber-file?
Soroljon fel három NYÁK-tervezési ökölszabályt!
- A vezetékeink legyenek 8 mil-nél vastagabbak.
- A tápvezetékek legyenek a jelvezetékeknél 4-5-ször vastagabbak.
- Lehetőleg ne használjunk 0,6 mm-nél vékonyabb furatokat.
- A furatok szélesebbek legyenek, mint a beléjük helyezendő alkatrészlábak (0,1-0,2 mm-rel).
- A panel széléhez 1 raszternél közelebb ne tegyünk furatot.
- A vezetéket ne derékszögben, hanem csak 135°-ban hajlítsuk.
- Használjunk szabványos furatátmérőket.
Mi a via és a pin?
- Via: Két vezetékezési réteg között fémes kontaktust teremtő furat.
- Pin: Pinnek nevezzük egy huzalozás végpontját a kapcsolási rajzon és a huzalozási rajzon egyaránt. Általában ez egy alkatrészláb szokott lenni, de lehet akár egy mérőpont is.
3. Hálózati szűrő
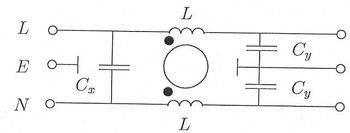
Egy hálózati szűrő kapcsolási rajza az alábbi ábrán látható:
Adja meg a szűrő aszimmetrikus zavarjelre vonatkozó érvényes modelljét! Ideális elemeket feltételezve írja fel a szűrő csillapítását aszimmetrikus zavarjelekre!
- Aszimmetrikus közös módusú
- rövidre van zárva
- A két tekercs párhuzamosan van kapcsolva, vasmagjuk közös 1db L induktivitású, dupla vezetékvastagságú tekercsként modellezhető
- A két az és a föld közé párhuzamosan van kapcsolva
- Tehát a szűrő aszimmetrikus zavarjelekre vonatkozó csillapítása:
4. Hall-szondás árammérő
Írja le a váltakozó áramú árammérő lakatfogó és egyenáramon is használható Hall-szondás árammérő lakatfogó működési elvét!
A lakatfogó egy olyan áramváltónak tekinthető, melynek primer tekercse 1 menetszámú. Ez az a vezeték melynek áramát mérni szeretnénk. A szekunder tekercs pedig egy zárt, de egy ponton nyitható vasmagra van csévélve. Az I áram a vezetékre koncentrikus H mágneses térerősséget kelt, ami közegben azonos irányú B mágneses indukciót hoz létre, amely a szekunder tekercsben feszültséget indukál - RAJZ!
5-6. Mérőerősítő
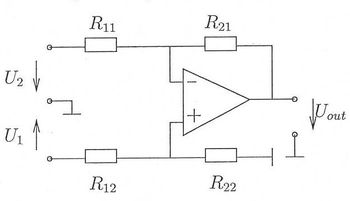
Az alábbi ábrán egy mérőerősítő elvi kapcsolási rajza látható.
Az ellenállások adatai:
- - Az ellenállások tűrése
Az erősítő adatai:
- - Az egységnyi erősítéshez tartozó határfrekvencia
- - Fázistartalék
Határozza meg a fenti kapcsolás:
- (a) eredő szimmetrikus feszültségerősítését
- (b) az erősítés statikus hibáját
- (c) közös feszültségerősítését
- (d) eredő (-3 dB-es) felső határfrekvenciáját!
Eredő szimmetrikus feszültségerősítés:
Erősítés statikus hibája:
Közös feszültségerősítés:
Eredő (-3 dB-es) felső határfrekvencia:
Határozza meg a domináns pólus törésponti frekvenciáját úgy, hogy a visszacsatolt erősítő amplitudómenete maximálisan lapos legyen!
Határozza meg az erősítő kimeneti feszültségének várható szélső értékeit, ha az erősítő előzőleg ki lett ofszetelve, és az erősítő bemeneteire a következő feszültségeket kapcsoljuk:
7. A/D átalakító
Adja meg egy A/D átalakító SINAD paraméterének számítási módját az idő és frekvenciatartományban!
Definiálja az összefüggésben szereplő mennyiségeket! Hasonlítsa össze a két számítási módszert!
Időtartomány:
Frekvenciatartomány (J - alapharmonikus):
8. Fáziszárt hurok
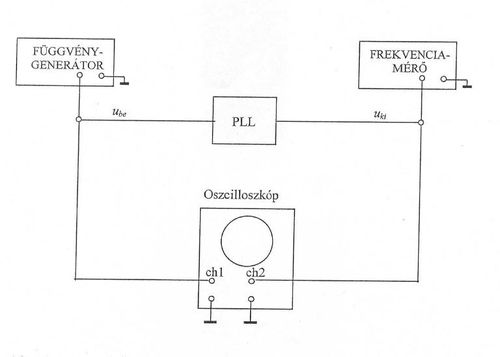
Fáziszárt hurkok esetében mit értünk befogási és követési tartomány alatt? Rajzoljon fel egy mérési elrendezést, amellyel meghatározhatja a befogási és követési tartományt!
- Követési tartomány (HOLD-IN): Az a frekvenciatartomány, amelyen belül a PLL követni képes a bemeneti jel fázisát, miközben a bemeneti frekvencia az frekvenciától távolodik. Ezt a követési tartományt a hurokelemek telítésbe jutása korlátozza.
- Befogási tartomány (PULL-IN): Az a frekvencia tartomány, amelyen belülre kerülve a PLL képes elérni a fáziszárt állapotot.
9. Szemábra
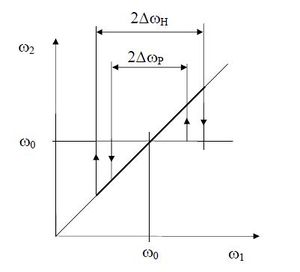
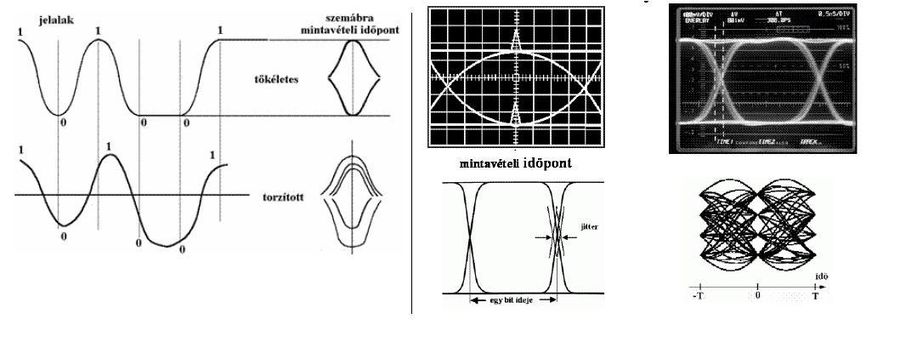
Mit értünk szemábra alatt? Rajzoljon le egy tipikus szemábrát! Mitől "szűkül" be egy szemábra?
Amennyiben az átviteli csatorna nem ideális, az elemi jel időfüggvénye torzulni fog. Ennek eredménye, hogy az egyes mintavételi helyeken nem csak az adott elemi jelnek lesznek hozzájárulása.
Az ISI és a zaj az oszcilloszkópon láthatóvá tehető, ha a vett jelet 1/Tb vízszintes eltérítési sebességgel ábrázoljuk.
Torzítatlan jelalak esetén a vett jel valamennyi Tb időtartamú szakaszát egymásra rajzoljuk, akkor nyitott szemet kapunk. Torzított esetben nem pontosan a +1 és -1 ponton halad át a jel, így a szem beszűkül, nehezebb lesz a jel detektálása.
10. Állapotteres szabályozás
Adott egy folytonos idejű szakasz állapotteres leírása:
A szakaszt állapot-visszacsatolással kompenzáljuk, ahol K = [2 4]. Adja meg a szakasz és a zárt szabályozási kör sajátértékeit (pólusait)! Stabil-e a szakasz, illetve a zárt rendszer?
A szakasz karakterisztikus egyenlete:
Melynek gyökei a szakasz pólusai (sajátértékek), azaz és . Mivel valós része pozitív, ezért a szakasz instabil.
A zárt rendszer állapotegyenlete behelyettesítés után:
A zárt rendszer sajátértékeit az (A-BK) mátrix sajátértékei adják:
.
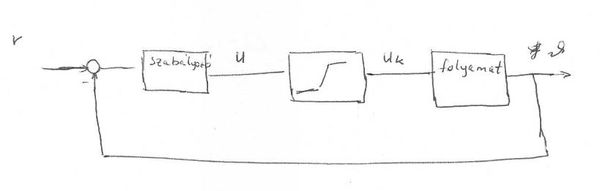
11. Hőmérséklet-szabályozás
Vázolja fel a digitális hőmérséklet-szabályozási kör blokkvázlatát! Tüntesse fel a jelek elnevezését, jellegét és dimenzióját!